The old new math
 In the early 70’s everyone learned a little bit of new math in elementary school. Sets, Venn Diagrams, different bases… Little did we know, little did we care where it came from, or that it had not always been part of the curriculum…
In the early 70’s everyone learned a little bit of new math in elementary school. Sets, Venn Diagrams, different bases… Little did we know, little did we care where it came from, or that it had not always been part of the curriculum…
(*You can read a bit more about New Math all the way at the bottom of this post.)
(Follow up: discussion on what topics to add and remove from the curriculum right here.)
I know they stopped teaching it. Kids don’t know what a set is anymore. Still, it’s one thing to know, another to see the blank looks on their faces. Strange.
Thursday I was planning to teach compound inequalities to my freshmen. My (excellent) Algebra text (Dolciani et al) has a little side unit on union and intersection. So I decided to squeeze my lesson into the last 5-10 minutes, and teach some old new math instead.
I started by putting a big
and a big
on the board. I asked if anyone knew what the symbols were.
In my school the kids come from a wide variety of middle schools, and many from honors or accelerated programs. So there was a chance. I expected about a third of the hands to go up. Only three did. I asked who would be willing to wager some points on the next test that they really knew.
Would they wager some points? All the hands went down.
Then we talked. Their time for fun. Cold war. Who lost China. Nazi scientists. Sputnik. Laika. Gagarin. New Math.
Then it was my turn for some fun. Quick and dirty I defined set. Gave a few examples. Defined cardinality since they like to think they are learning big words. Defined the empty set. Defined subset (and a bit later distinguished between proper and improper subsets). Heard a kid saying that it was like “less than” and smiled; I came back to that later.
The high point occured after I put this on the board:
I asked them if the statement were true or false, and to write down their answer and their explanation. We had a spirited little discussion, but most of them followed the model (since there is no evidence that V is not a subset of R, it is a subset of R)
Finally we spoke a bit about intersection and union, their relationship to “or” and “and,” to multiplication and addition. I promised them that if they took logic with me when they are juniors or seniors…. but there was hardly time left for the lesson.
(New Math was an attempt to add some early theory, mostly axiomatic sort of stuff, for younger kids. Idea was, when they got older and hit advanced topics, they could already handle some of the rigor. It was a response to Sputnik, to the Soviets getting into space first. They claimed it was because the Soviets had more and better engineers, and that was because the little Soviet children learned set theory. Hmmph)
(New Math floundered for taking itself way too seriously. A little bit of sets and venn diagrams and bases would have been cool. But they put in way too much for most students, and got way too complex way too young for most students)
Wikipedia’s article on New Math used to say that it was making a come back. Too bad, in a more moderate form, there was value to kids’ getting exposed to sets and some related concepts. But, no, it’s not so, not coming back in its original form, not coming back more modestly.


Great thoughts.
I remember New Math from my elementary school days in the mid 60’s. I was aware at the time that a lot of adults thought it was a strange and incomprehensible way to teach math — which I never understood, since sets, as we learned them, seemed a pretty obvious concept.
But looking back, the whole idea that you should teach the axiomatic foundations of math to elementary kids seems misguided. I certainly didn’t “get” that side of it — it just seemed like adults making a big deal about something obvious.
— Rachel
The point at which the axiomatic foundations of math began to make sense was when we discussed non-Euclidean geometry in high school, and talked about how variants of the 5th (?) postulate produced different geometries.
New math, new new math, old new math…. I just don’t understand why the concept of balance often seems to be foreign and/or unacceptable to people. The extremes rarely work well. Taking the best of both worlds could get us where we want to go.
By the way, I liked your lesson.
I remember sets from high school math (mid-90’s). Well. I remember the *word* sets from high school math.
I must be young enough to have missed the trend for teaching sets in grade school, but I remember my precalculus teacher introducing us to the set notation and operations in our junior year. It seemed obvious.
e: I agree. It seems that there have been a number of good ideas in math education over the years. The primary flaw has not been with any particular idea but with people’s preoccupation with relying on one exclusively.
Henri Picciotto quotes Tofu Roshi: “There is no one way.”
I definitely worked on sets in 2nd grade, but I think we also did them in K and 1st (different school system). I will ask my younger sister. We were at the tail end. I remember them being easy, and fun, except I had trouble keeping the symbols straight.
I confused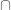 with
with 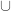 and
and 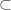 with
with 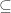 much as I confused less than and greater than and left with right, and later sine with cosine, and whether “personne” preceded the preterite and “rien” came after, or vice versa (it is vice versa, reverse abc order was my device to remember, and then instinct from getting it right so many times)
much as I confused less than and greater than and left with right, and later sine with cosine, and whether “personne” preceded the preterite and “rien” came after, or vice versa (it is vice versa, reverse abc order was my device to remember, and then instinct from getting it right so many times)
I think they should bring some set theory back.
I wish I had seen this post first before responding to above.
I did not know that set theory is not typically included in any math standards in the US. Singapore has a short treatment of it in the 8th or 9th grade, but does not advance it to proving set equalities, for example.
The SMSG texts that I have use set theory as a tool with which students could understand algebra and calculus and don’t relegate it to an introductory chapter never to be revisited like what evidentally was done in the elementary grades in many of the commercial texts of that era. At any rate, by algebra II the kids used set notation and and field axioms to prove scores of theorems. It seems to have nothing to do with the current math wars at all. It is neither “drill and kill” nor “constructivist.”
The most interesting exercise in the ninth grade algebra book out of which I taught was one in which the student is asked to complete a series of problems which lead to the “discovery” of the cardinality of the power set.
I don’t know anything about the Soviets using set theory in K-10 education (at the time they didn’t go to grade 12 like we do) There are articles online which state that Kolmogorov, when asked to reassess Soviet math education specifically rejected set theory because it was something that most of their teachers weren’t familiar with at the time.
Table of Contents for “New Math” algebra I:
http://www.oplink.net/~adrian/allen_pearson_alg_1.html
Table of Contents for “New Math” algebra II:
http://www.oplink.net/~adrian/allen_pearson_alg_2.html
I’m the Space Race generation–we did New Math through elementary and high school in the 60s. Our parents hated it. They didn’t have a clue what we were doing. And it was more than set theory. We did bases, and focused on process, what we were doing when we divided or multiplied. It had its weaknesses, but it was at least math, unlike what the NCTM favors these days.
I was tail-end (entered K at the very end of the 60’s). The sets are most obvious to me, since my students now have none. There was also incredible amounts of place value work, decomposition of numbers, and non-standard variants of standard algorithms, used to introduce the standard algorithms (not instead of…) My mom saved a box of papers, not only math, but I found a wonderful bit of introductory long division… if I can reproduce it, I will. If not I guess I can scan and upload.
It’s not safe to draw conclusions based on my own, personal experience, but the New Math worked well for me, gave me far better control over numbers and process than I would otherwise have had, and set the stage for strong algebra, etc.
“I found a wonderful bit of introductory long division… if I can reproduce it, I will. If not I guess I can scan and upload”
Sweet.
A basic understanding of sets is needed for the SAT exam. I am a high school math teacher and work as an SAT tutor on the side (not for kids from my school). I am consistantly blown away by the fact that seniors in high school have no concept of a what a set is. The SAT covers intersection, union, subsets, and cardinality albeit all in a very cursory way.
You wrote: “New Math was an attempt to add some early theory, mostly axiomatic sort of stuff, for younger kids.[…]. It was a response to Sputnik, to the Soviets getting into space first. They claimed it was because the Soviets had more and better engineers, and that was because the little Soviet children learned set theory.”
At that time, little Soviet children did not learn set theory. I know that — I was one of them. A good idea of the kind of mathematics taught in 50-s at Soviet schools gives Kiselev’s Geometry, now available in English translation from http://www.sumizdat.org/
Alexandre and Myrtle address Soviet mathematics from the 1950s and 1960s. I have a friend (b 1962) who went to a “special math school” in his medium-sized Soviet city, and swears he had some set basics in his education.
Perhaps he is wrong (though we need the algebra / arithmetic texts, not geometry). In any event, our “theorists” thought we should add some sets to be able to introduce theory earlier, to create a generation of superior engineers. Didn’t really work, though I may have personally benefited.
So how do we find the primary level Soviet math books?
I found this discussion accidentally (and 2 weeks late) by tracking back the link Alexandre Borovik provided to my website http://www.sumizdat.org, and so I am not sure why you were discussing “new-math” and wanted primary level Soviet programs, but let me try to add my 2 cents (sorry if they turn out to be off the subject).
A currently popular in Russia primary math program goes under the name “Peterson” (although it was started jointly with late Naum Vilenkin) and can be purchased at the Russian version of Amazon.com:
http://www.ozon.ru/context/detail/id/1195816/
It is not Soviet, but post-Soviet program and, too bad, it is
in Russian. The good news: Singapore Math is in English and
is simpler (and hence better, to me) than “Peterson.”
As about set theory, the recollection of your friend about “special math school” in Russia is correct. Such schools appeared around
1960, and an in-depth study of mathematics and physics was quite
usual there. E.g. in my school (Moscow school #2, grades 7-10, 1971-75), in addition to the standard courses in Algebra and Geometry, taught concurrently in each grade, we had minicourses
in logic, set theory, number theory, combinatorics, abstract algebra
(several chapters from Van der Waerden), and 2 years of one-variable analysis. However, in – for example – set theory,
we would not stop at de Morgan rules, but would establish 1-1-correspondences between N,Z and Q, between R and R^2, and
prove non-countability of continuum. Here is my point: math is
full of “concepts,” but they are there not for their own sake but to represent knowledge. A lot of (so called) math, “new” or “old,” taught in US schools is content-free. “Excellent” texts by Dolciani et al supply
enough examples of this.
Next, Russia did have its “new math” reform, and it was initiated by
Kolmogorov around 1975. It relied on 15 years of very encouraging experience in “special math schools” and in this sense was perhaps much better prepared than that in the US. The idea was to introduce to school some modern math, and in particular to build geometry around the concepts of geometric transformations.
The reform was an immediate and spectacular disaster of which math education in Russia has never fully recovered. Three key reasons can be cited:
– after sudden shift in terminology, parents could not help their kids;
– teachers were not ready either;
– lots of meaningful math exercises accumulated over decades suddenly became useless, and were urgently replaced with tautologies, resulting in sudden drop of general math culture.
The moral of this story should be: (math?) education is a
conservative area where *any* reforms are disastrous.
Thank you. Your discussion of the 60’s – early 70’s matches my friend’s experience closely (though in a smaller city). American readers likely do not realize that algebra and geometry were taught concurrently.
Your description of Kolmogorov matches part of our “new new math” reforms (switch emphasis to transformational geometry).
I am a bit confused. Are you critical of the Dolciani texts?
As far as I understand, “new new math” refers to the reform of 1989-2006 based on the “NCTM standards” (and called often “fuzzy math”, or “constructivism” depending on a camp). If so, believe me:
it has absolutely nothing to do with Kolmogorov’s reform in Russia.
Kolmogorov’s reform was done by mathematicians (and not by cognitive scientists), it had the same noble goals of bringing relatively recent math into the classroom as the “new math” reform of 1960-70 in the US, it was mostly concerned with middle-to-high school curriculum, and it produced a reasonable set of textbooks – reasonable, but not great (as any first generation of texts would be), and it interrupted the tradition and well-tested routines, and thus failed. I don’t see any relation with “new new math.”
As about Dolciani’s texts: yes, I am critical of them. I saw old (perhaps of about 1970) books of high school level – they were not
great, but sort of OK, especially compared to the modern ones.
Of the recent ones, I have “Prealgebra, accelerated approach”, and
had a chance to examine some volumes of Algebra I “Structure and
Method” (which are quite similar to the Prealgebra text) – they all pave the way to math ignorance of the students, and do this quite
efficiently.
What do you thin of them?
The geometry reform you wrote about shares an emphasis on transformational geometry with the our new new math. Further, as a reader here pointed out, the broad outlines of new new math were painted in a 1980 article by Usiskin (you can read it here which sounds even more like your description of Kolmogorov. This reform looked even worse when it was implemented. Both of our big math reforms were aimed primarily at the lower grades. New, new math barely reached the high schools, and was met with fierce opposition. It still hangs on in elementary schools, and may actually be gaining ground in middle schools, where no one has figured out how to effectively use the time between fractions and variables.
Yes, I use the Dolciani Algebra and Algebra II w/Trig texts. I am quite happy with them. I have not seen the prealgebra. I have no idea what you are saying when you call them “content-free” or that they “pave the way to math ignorance.” Perhaps such rhetorical flourishes are effective when making sales to home-schoolers. It is easy to appeal to an engineer’s sense of mathematical superiority.
The Dolciani texts are a bit boring. The material logically develops from one section to the next. (iow, the mathematical content organizes the book s correctly). The exercises come in a range of difficulty. They suit our needs.
I followed your link to Usiskin (thank you). I haven’t seen Usiskin’s geometry text, but it is possible that it carries some resemblance with those of Kolmogorov’s reform, in the sense that both would emphasize geometric transformations. However I can confirm that Usiskin’s reform proposal and especially his motives have little to do with Kolmogorov’s.
Russia has never had the problems Usiskin tried to resolve.
2D geometry was taught out of a 200-page book over a course of
3 years (to get an idea, you may check >50 sample pages of Kiselev’s Geometry at http://www.sumizdat.org), and 3D geometry – out of 100-page book over 2 years, so there was hardly any time shortage. Geometry used to be (and probably still is) by far the favorite math subject of most students there. There had never been such things in Russia (nor in real math as a matter of fact) as “formal proofs,” “2-column proofs,” as well as there was no idea to teach math “without proof” (proofs just answer the question *why* what is true is true, and the “why”s were taught from grade 1, whether one calls them proofs or not). And the rhetoric didn’t change: geometry is still taught in Russia because it teaches creative and critical thinking, logic, develops intuition and problem solving, and other indispensable learning skills. Thus the motive of “new new math” to get rid of boring, formal, senseless routine didn’t apply to Kolmogorov’s reform.
As about you having no idea what I mean by “content-free” and “paving the road,” I can explain.
Union and intersection of sets are just names – there is no knowledge
in giving names to things (Shakespeare knew this: “What’s in a name?”) Learning de Morgan rules and stopping there is not worth
the effort because the rules are tautologies: trivial (although non-obvious at a first glance) consequences of definitions. There is no knowledge (hence no mathematics) here – the subject is content-free.
Unfortunately a lot of math teaching in the US does just this.
One introduces the name “perimeter” and makes the kids to add
numbers written on the sides (“find the perimeter of a hexagon with
sides 2,3,4,5, 7, 22”), forgetting that there is no geometry here.
The geometry section in Dolciani’s et al “Prealgebra” (and I believe
in Structure and Method too) is 15 content-free pages, the most
spectacular of the exercises being: Find the angles of a regular
6-gon *given that the angle sum of a 6-gon is 720 degrees*.
Another disease of the US math education is presenting math as
a collection of hundreds of unrelated facts and routines. Parents with
“engineer’s sense of mathematical superiority” teach their children that factoring a polynomial is the same as finding its roots, teach how
to derive Vieta’s formulas, the quadratic formula, the method
of finding all rational roots of a polynomial with integer coefficients,
and how to use them interchangeably for factoring and/or equation solving. Dolciani et al manage to write 3 (!) chapters on factoring quadratic polynomials with integer coefficients, according
to 3 “cases”: the free term =0, the top coefficient =1, the top
coefficient not equal to 1, and make students exercise in such factoring even before and with no connection to solving quadratic equation.
There are some other fundamental misconceptions about math in
the US education. It is a long discussion; for a shortcut, I am putting on the web a letter I wrote 2 years ago to a school headmaster (about specific textbooks he was interested to discuss). Don’t judge it too harshly – the letter was not intended for public eye, but it addresses some of the issues:
http://math.berkeley.edu/~giventh/academy.html
Representing math the way opposite to what it really is most certainly paves the road to math ignorance. Each particular act
probably does not matter, but being exposed to nonsense on a
daily basis for 13 years, most students get the message: math is
a chaotic and nonsensical manipulation with words and symbols.
Unfortunately I don’t have much chance to discuss this issue with homeschooling parents, but products of our regular school system
fill in my classrooms in Berkeley.
what the device called
I loved the New Math. Kurt Goedel is definitely the Einstein of Mathematics’s Logic Field. I used to be able to find the Russian Series
of Math called Topics in Mathematics. It was neat in that each topic
was in a colorful pamphlet that covered New Math but in an accessible way. Much like the Math Competitions from Waterloo University in Canada or for those with a stronger urge to problem solve the Olypiads or Putnam (these competitions are age restricted and by background since obviously as one ages ideas become more accessible and less unwieldy – perhaps Olympiad is an inappropriate title, since the knees go first then the hairline and of course the libido!).
It would be great to see these Translated works in the Google Digital library.
Gus.
I’m curious. Can you tell us more about the Russian books? Can I find them anywhere?