More on the roots of i
In this post I mentioned looking for , and in this comment mentioned searching for
. In this comment, reader Vlorbik took exception, and said that I would have better looked for
, and then more comments which I was not certain I understood. And then yesterday one of the top puzzle solvers here, JBL, weighed in, saying in effect that my error was small.
it is the math that holds the authority, not me
I want my teaching to be well-informed, so I dug around a bit (spoke to a professor, dipped through a couple of books, surfed). Check my understanding, if you will.
(Discussion continues, beneath the fold –>)
When we extend the Natural numbers to include an additive identity, and then to the Integers, and thence the Rationals, and finally the Reals, we preserve order. But when we extend to the complex numbers, we lose order. If you haven’t thought about this before, consider complex numbers, a+bi, graphed on Real vs imaginary axes. (image from
(image from
Weisstein, Eric W. “Complex Plane.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/ComplexPlane.html)
Because we are in a plane, not on a line, we do not have a “greater than” direction. Think about this:
could we say which was greater, 4 – 3i, 3 – 4i, -3 + 4i, -4 + 3i, 5i, -5i, 5 or -5?
(digression): When the very first New York State Math B Regents (June 2001) included this question
Melissa and Joe are playing a game with complex numbers. If Melissa has a score of 5 – 4i and Joe has a score of 3+2i, what is their total score? (question #11)
I knew we were in serious trouble. Contriving real world contex was trumping mathematical sense. Insteading of asking students to add two complex numbers (a bit easy, but still a question one might ask), a highly improbable situation (keeping score with complex numbers – not if it is important to know who is in the lead!), was paired with a silly task (add up scores? only if I am looking at the under/over, right?). But let’s leave the NYS Regents for other discussion. (/digression)
Lets return to what was wrong with my beginning: . Had I written on the board
, I would have wanted the kiddies to respond that the value was 5, since there is an implied principal square root. If I wanted both roots, I would have prompted them instead with
.
This is where Lisa Simpson makes her mistake in the separate boy/girl math episode, Girls Just Want to Have Sums. She shouts (from the bushes!) “5.” Let’s pause to solve this.
or, shorter version:
.
So, had I asked for the solution to , we would be hunting for two roots. But since I asked for
there is an issue with the idea of principle root, and
is better since it asks for both, but there is something off, since I don’t know which is the positive and which is the negative root.
Let’s stick with the unambiguous. No harm there: . Plus it is a fantastic tease to have gotten a preview with (increasingly cumbersome) algebra. This group will be learning DeMoivre’s theorem in the fall term next year.
OK, I started explaining my error to the class on Friday. We will take a second shot at it sometime next week. There is something else, very positive, at play here. I am a math teacher. I communicate to the students. But there is math I don’t know, math I continue to learn, and in the end it is the math that holds the authority, not me.

Yes! Sharing the process with students of how you go about solving problems or asking questions feels really good to me. It’s a way to teach them how to think instead of just teaching them facts and procedures.
It is true that the complex numbers are not ordered, but it is possible to identify a principal value for the square root, as explained in the Wikipedia article. In short, we represent the complex number in polar form z = r e^(it), where t is between -pi and pi (including pi) and r is a non-negative real number. Then the principal square root of z is r^(1/2) e^(it/2). However, I should caution that this convention is not universal.
Thanks for the encouragement and clarification. I will include this bit in my explanation to the class, though I do intend to avoid the symbol when working with complex numbers. It’s not worth the ambiguity, however slight, when there is a completely unambiguous approach available.
symbol when working with complex numbers. It’s not worth the ambiguity, however slight, when there is a completely unambiguous approach available.
There are two problems with identifying a principal square root function (or, in general, a “rational power” function) on the complex numbers: the choice of range is entirely arbitrary, and the function can’t be continuous everywhere. Neither of these is a particularly big problem, and much of the time it works fine to use a function equivalent to the one involution suggests.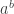 where
where  is anything other than a (real) rational number represents infinitely many values.
is anything other than a (real) rational number represents infinitely many values.
Things start to get nastier as we extend to nonrational powers: in the complex numbers, an expression
It’s been a while, but don’t the nth roots of unity form a group under multiplication, if n is rational, but do something strange if n is not?
Where does the +- come from?
y^2=25 =>
(+y)^2=25, (-y)^2=25 =>
sqrt(y^2)=sqrt(25), sqrt((-y)^2)=sqrt(25) =>
y=5, -y=5
Jonathan: Yes. I think the easiest way to get a feel for what is going on is to exchange the notion that a positive integer power is what you get by repeated multiplications, which extends to reasonably natural explanations of nonpositive integer and rational powers, to the understanding of exponentiation in the complex numbers, best understood in terms of the exponential function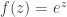 .
.
We have . If we raise this to some rational power, we get
. If we raise this to some rational power, we get  raised to a bunch of numbers which are rational multiples of
raised to a bunch of numbers which are rational multiples of  , with constant denominator. As we go down the list of values for 1 that I’ve written above, we’ll see that these values eventually “wrap around”: we start getting values where the exponents differ by an integer multiple of
, with constant denominator. As we go down the list of values for 1 that I’ve written above, we’ll see that these values eventually “wrap around”: we start getting values where the exponents differ by an integer multiple of 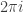 , and these will actually give us the same value. So, finitely many values, which geometrically can be seen to lie at the vertices of a regular polygon inscribed in the unit circle centered in the origin. (We know which such polygon because it includes 1 as a vertex.) And these values do indeed form a finite cyclic group under multiplication.
, and these will actually give us the same value. So, finitely many values, which geometrically can be seen to lie at the vertices of a regular polygon inscribed in the unit circle centered in the origin. (We know which such polygon because it includes 1 as a vertex.) And these values do indeed form a finite cyclic group under multiplication. form an infinite additive cyclic group.) All the values must still have absolute value 1, and geometrically in turns out that they represent a dense subset of the unit circle.
form an infinite additive cyclic group.) All the values must still have absolute value 1, and geometrically in turns out that they represent a dense subset of the unit circle.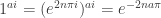 . Note that the exponent there is real: this actually describes an infinite set of real numbers, an exponential family. This again turns out to be an infinite cyclic group, and it doesn’t matter whether
. Note that the exponent there is real: this actually describes an infinite set of real numbers, an exponential family. This again turns out to be an infinite cyclic group, and it doesn’t matter whether  was rational or irrational.
was rational or irrational. . If a and b are not 0, the result will be the result of multiplying all the values from the corresponding cases. Geometrically, this gives you exactly what you would expect (a bunch of concentric circles, each of which looks like what you get when you do
. If a and b are not 0, the result will be the result of multiplying all the values from the corresponding cases. Geometrically, this gives you exactly what you would expect (a bunch of concentric circles, each of which looks like what you get when you do 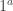 , with radii given by the values of
, with radii given by the values of 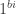 ); algebraically, it’s equivalent to the product of the two groups.
); algebraically, it’s equivalent to the product of the two groups.
In the case that we use an irrational real exponent, everything happens the same except for the “wrapping around”: no two multiples of an irrational number differ by an integer. For the algebraic structure of the roots, this means we still actually have a multiplicative cyclic group, but this time it will be infinite. (This happens in this case, as well as in the previous, because the exponents
The case of imaginary exponents is even weirder.
In order to get generic complex exponent, we just use the fact that
Unfortunately, I can’t preview, so I’ll have to wait to see how this turns out :-)
I’ll repeat this note elsewhere, but if you include some kind of flag at the end (eg, feel free to fix my latex), then I will, indeed, try to fix the latex, if I knew what you were after.
Alternately, you can post, and if you don’t like the result, post again, and again, until you are happy, and I will go in and delete the unsatisfactory early tries.
In the meantime, I am digesting the bits about the cyclic groups. Everything up to the imaginary exponents I once knew, so it’s not completely foreign.
Okay, thanks!
At some point in my last comment I used the words, “exponential family.” What I really meant was that the sequence is an infinite, two-ended geometric sequence. For example, if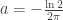 then
then  , where I’m using equal signs somewhat loosely here (the thing on the right should really be the set of all such numbers as
, where I’m using equal signs somewhat loosely here (the thing on the right should really be the set of all such numbers as  varies over the integers). And this set really is an infinite-at-both-ends geometric sequence, which also happens to form a multiplicative group. And this would work for any value of
varies over the integers). And this set really is an infinite-at-both-ends geometric sequence, which also happens to form a multiplicative group. And this would work for any value of  I happened to choose.
I happened to choose.
what about your
“study more analysis”
plan, though? did you
struggle through one
or more semesters like
you planned… or give
up in some “what would
owen do?” moment?
& if so, when? & how did
it feel? inquiring minds
want to know (and other
tautologies).