Puzzle: Who am I?
I must have posted this once before, but I forget. And two classes worked this last week. And had fun. So I’ll share:
There are five true and five false statements about the secret number. Each pair of statements contains one true and one false statement. Find the trues, find the falses, and find the number.
1a. I have 2 digits
1b. I am even
2a. I contain a “7”
2b. I am prime
3a. I am the product of two consecutive odd integers
3b. I am one more than a perfect square
4a. I am divisible by 11
4b. I am one more than a perfect cube
5a. I am a perfect square
5b. I have 3 digits
Can you solve this? Can you use it in your classroom?
In mine, I let kids flounder for 10 – 15 minutes (seems like an eternity), quietly dropping little hints… Finally (and finally in one class means after two kids stumbled into the answer, in the other class none had), I said “look, there’s not so many possibilites” and I began listing them (vertically):
| a | a | a | a | a | a | a | a |
| a | a | a | a | a | a | a | a |
| a | a | a | a | b | b | b | b |
| a | a | b | b | a | a | b | b |
| a | b | a | b | a | b | a | b |
Now, I was doing all the work, but saying it out loud, until one, then a few, then half of them were jumping in ahead of me. Every once in a while (and I created four of these, this starts aa, next ab, next ba, next bb) every once in a while I stopped and asked a quiet kid “what next?” — it’s hard to turn off teaching.
And then I asked them to start eliminating impossible variations, and they did. One class got down to 3, the other 4, and then they went back at them, with all this gained knowledge (and technique!)
I tried to keep them (fairly successfully, thank you) from telling each other the answer. And for the next two days I had a trickle of kids finding me in the hall and shouting the answer at me, excited that they’d gotten it.
If I could get the same enthusiasm for adding rational expressions….

I really like this and am going to steal it :).
(And I won’t spoil by posting the answer!)
The logic was fun on that. I’ll look forward to using this. (If I can manage to create a filing system that will help me remember this and find it when I need it.)
Do you remember where you found it?
Thanks!
Ta da!
That’s an original.
I offer very few of those. Most of my work is someone else’s older work that’s found it’s way into my classroom…
I once solved a much harder, my level version. I picked it up on the MatSci (or was it SciMat?) SIG on compuserve, back 15 or so years ago. I may have published that as well (going to look for the link…)
That’s impressive! Hmm, maybe I should try to make one…
Making them turns out to be a nice challenge. How can you be certain you have something possible? Something unique?
Should you start with a few pairs, and see what works? Should you start with the answer, and zoom in? Should you start with conditions, and work them down (less than 100, more than 50, so work each one of those statements into a separate pair… careful not to mate them with “even” and “odd” — forcing one to be false, etc, etc)
a. I am 1 digit
b. I am a perfect square
a. I am two digits
b. I am prime
Notice how we don’t need to talk about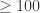 , because that would force bb, perfect square and prime, neat contradiction.
, because that would force bb, perfect square and prime, neat contradiction.
Or…. you could just translate it into another language. Italian’s already been done.
That was fun. I may try to use this at some point.
I came across this puzzle in the book “Playing with Math.” I found a different solution based on a wrong assumption I made at the beginning of solving the puzzle. I was thinking that a number with 3 digits also has 2 digits so I made both of those statements true and came up with 4097, which works for all the other conditions.
Sounds like a needed a few “exactly”s to make the solution unique!
I’d say ‘different interpretation’ instead of ‘wrong assumption’. I wonder how many solutions the puzzle has using your interpretation. (Pretty exciting to see my book has inspired new discussion on Jonathan’s blog post!)