Skip to content

Quiet Birthday

February 5, 2008 am29 8:39 am

p^2q,
First of two
in a row.

Friend, with the same birthday, called during class. No one calls during class. So I said “no one calls during class. It’s probably my friend with the same birthday as me, calling to remind me. He never forgets.” And it was.

Calls all day and evening from friends and family.

Highlight of the day was proving \sqrt{2} is irrational, and listening to kids arguing with each other afterwards. Now we know four kinds of proof. (as I had just introduced proof by cases, which isn’t a full type in its own right, but deserves separate mention all the same).

from → Math, Math Education, Math Teachers, mathematics, Puzzles, The Wide World
16 Comments leave one →
  1. Rachel permalink
    February 5, 2008 am29 9:53 am 9:53 am

    49? But no, that would be the 2nd of 3 in a row…

    Reply
  2. jd2718 permalink*
    February 5, 2008 am29 10:01 am 10:01 am

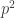    49 is p^2, and I seem that old, huh?
    We are looking for p^2q

    Reply
  3. jd2718 permalink*
    February 5, 2008 am29 10:28 am 10:28 am

    Dave Marain’s father would have been 100…

    Reply
  4. jose permalink
    February 5, 2008 pm29 3:00 pm 3:00 pm

    Happy belated, man. Got caught up with everything else but when I saw Facebook, I knew I missed it. Sheesh. And is it 36?

    Reply
  5. jd2718 permalink*
    February 5, 2008 pm29 4:26 pm 4:26 pm

    Thanks. And more belated than that, in return. 36 would be p^2q^2, so no.

    Reply
  6. mathmom permalink
    February 5, 2008 pm29 7:05 pm 7:05 pm

    Happy belated birthday! Your powers of 2 comment gave it away. You must have been born in ’64 making you 44 yesterday where p=2 and q=11. Next year you will turn 45 so P=3 and q=5.

    Reply
  7. Alane Tentoni permalink
    February 5, 2008 pm29 11:13 pm 11:13 pm

    Hope you had a super day yesterday!

    Is that your logic class doing proofs? Sounds like fun!

    Reply
  8. Nathan permalink
    February 6, 2008 am29 1:29 am 1:29 am

    I’m totally lost where you are getting the p and q. And happy birthday – I love your blog!

    Reply
  9. jd2718 permalink*
    February 6, 2008 am29 4:12 am 4:12 am

    Thanks, Nathan,

    I’m using p and q to represent prime numbers.

    So 33 is pq, 34 is pq, 35 is pq and 36 is p^2q^2 It’s all about the prime factorization.

    Reply
  10. Jackie permalink
    February 6, 2008 am29 6:33 am 6:33 am

    Students arguing about proof – I can’t imagine a nicer way to spend a birthday. Okay, perhaps I can, but… Happy belated Birthday!

    Reply
  11. Nathan permalink
    February 6, 2008 pm29 7:37 pm 7:37 pm

    Thanks, I guess I’m used to the older notation of p-subscript 1, p-subscript 2, etc.

    Reply
  12. e permalink
    February 6, 2008 pm29 8:02 pm 8:02 pm

    I’m missing important dates. I should work less and read more. Happy bb.

    Reply
  13. jd2718 permalink*
    February 7, 2008 am29 1:10 am 1:10 am

    Nathan, they are exponents, not subscripts.

    And thanks to all of you.

    Reply
  14. mathmom permalink
    February 7, 2008 am29 1:50 am 1:50 am

    I think Nathan meant that he would expect two distinct primes to be represented by p_sub1, p_sub2, etc. rather than p,q,…

    Reply
  15. Stella permalink
    February 7, 2008 am29 3:44 am 3:44 am

    44 = 2^2 x 3 45 = 3^2 x 5 I remember celebrating those two birthdays!!!!

    Reply
  16. jd2718 permalink*
    February 9, 2008 pm29 9:20 pm 9:20 pm

    Nathan, let me try this:
    p_1^2p_2
    And Stella, thanks for making me sound young!

    Reply

Leave a reply to Nathan Cancel reply