Thanksgiving Combinatorial Puzzles
In Combinatorics today students worked in groups of 2 or 3 on a set of 6 puzzles. The rules and puzzles are printed beneath the fold.
Several have already appeared on this blog. Sorry for the repetition. And one is much harder than I intended. Can you find it?
And that turkey? Links to a page full of Thanksgiving word searches, crosswords, jig saws… ie, real Thanksgiving (non-combinatorial) puzzles.
Click for my worksheet —>
There are six puzzles, worth 60 points each. The points for each puzzle will be evenly divided among the groups solving that puzzle. A homework pass will be awarded to all the members of any group scoring 40 or more points.
Good luck!
Puzzles:
1. At Thanksgiving dinner, there is turkey, cranberry sauce, stuffing, yams, mashed potatoes, and carrot casserole. How many different plates can be prepared if each plate has at least 2 items?
2. Four husband-wife couples will sit around a round table.
a) How many seating arrangements are possible?
b) How many boy-girl seating arrangements are possible?
c) If they try out each possible boy-girl seating arrangement for 20 seconds, how long will it be until they start eating?
3. Four husband wife couples will sit around a round table. How many seating arrangements are possible without any spouses sitting next to each other?
4. There are eight people sitting around a round table. They all jump up to get food, and in their rush to start eating, they carelessly sit in the first seat they come to. How many ways could they all end up in new seats?
5. There are eight people sitting around a round table. They all jump up to get food, and in their rush to start eating, they carelessly sit in the first seat they come to.
a) How many ways could exactly 2 of them end up in new seats?
b) How many ways could exactly one of them end up in a new seat?
c) How many ways could none of them end up in new seats?
6. There are eight people sitting around a round table. Each person reaches out to shake hands, and as they are shaking, they freeze. The most popular woman (a math geek) points out that there are four hand shakes going on, but that none of their arms are crossing. How many ways can this be done?
JD2718 
For the “how many seating arrangements” puzzles, are we to assume all seats are distinct, or are rotations/reflections of prior arrangements not considered new arrangements?
Rotations are not distinct, but reflections are.
Thanks – I’m giving these to my seniors today!
The first time I read problem 3, I interpreted it as no two wives or husbands should be seated together. That is one whole new problem to add to your list.
#3 is at a different level of difficulty from the rest, I think. It was a mistake. They might have had luck hand-counting if I had held it down to 3 couples.
#4 looks difficult, but it is something I taught in the last few weeks, so it was just an exercise (albeit a detailed one).
#5 I like for requiring thinking.
#6 I like for requiring hand-counting (don’t see any other way)
#6 doesn’t require hand-counting, it’s the fourth Catalan number. =)
There’s gotta be one in every bunch!
A very nice challenge for someone who recognizes what Brent did is to establish a 1-1 correspondence between the number of ways 2n people, arranged in a circle, can shake hands without crossing arms and the number of ways a hexagon can be triangulated.
Catalan numbers were the path for me to learn that counting stuff is not only fun, but is considered serious math.
I forgot to give proper credit when I gave these problems to my kids. Sorry.
Do you have soluions available to the Thanksgiving Combination Questions that you would be willing to share?
1. Several solutions. There are 6 items. And each item can be included or left out (that’s 2 choices each). If we are talking about carrots and stuffing, that’s neither, just stuffing, carrots alone, or both. 4 choices. (2 choices times 2 choices).
For 6 items, that will be 2 times 2 times …. or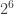
, which is 64 choices.
However, one of those choices is an empty plate. No good. And, 6 of those choices have just one item. No good either.
That leaves us with 64 – 6 – 1 = 57 possibilities. That’s near the high end of what I will ask kids to write out by hand.
Which other questions would you like solutions to?
Would it be possible to share your solutions for problems 2-6? Thanks. Perfect for my students by the way!