Skip to content

And the answer is…

October 29, 2007 am31 9:23 am

\sqrt{\pi}

Can you come up with a question?

(JBL has me busy on those bitstring, er, run permutation questions…. it could be a bit before I can really concentrate on a post)

from → Math, mathematics, Puzzles
17 Comments leave one →
  1. Rachel permalink
    October 29, 2007 am31 10:25 am 10:25 am

    What is the radius of a circle of area pi squared?

    Reply
  2. Pseudonym permalink
    October 29, 2007 am31 10:55 am 10:55 am

    What is the factorial of 1/2?

    Reply
  3. jd2718 permalink*
    October 29, 2007 pm31 3:30 pm 3:30 pm

    No? Not really, is it. Here’s what Google says (plunk it in the search line, and if it looks math-y, Google evaluates it):
    (1 / 2) ! = 0.886226925

    Reply
  4. JBL permalink
    October 29, 2007 pm31 4:58 pm 4:58 pm

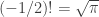    It should be \Gamma(1/2) = \sqrt{\pi}, which is sort-of equivalent to (-1/2)! = \sqrt{\pi}. (That’s the gamma function, for those who are interested.) Naturally,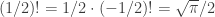 (1/2)! = 1/2 \cdot (-1/2)! = \sqrt{\pi}/2

    Reply
  5. Clueless permalink
    October 29, 2007 pm31 5:31 pm 5:31 pm

    Given a grid of lines spaced 1 unit apart, and a needle of length one unit, what is the square root of the average number of times the needle has to be dropped on the grid in order for it to touch or cross two lines.

    Reply
  6. mathmom permalink
    October 29, 2007 pm31 5:56 pm 5:56 pm

    There’s really such a thing as factorials for fractions? Who knew?

    Reply
  7. mathmom permalink
    October 29, 2007 pm31 5:58 pm 5:58 pm

    What is the side length of the square whose area is equal to that of a circle with radius 1?

    Reply
  8. Clueless permalink
    October 29, 2007 pm31 7:18 pm 7:18 pm

    What is the fourth root of the summation from k=one to k=infinity of (6/k^2) ?

    Reply
  9. vlorbik permalink
    October 30, 2007 am31 3:16 am 3:16 am

    “the cube root of 2”
    and “the cosine of 10 degrees”,
    cannot be constructed with
    compass and straightedge–
    this disposes of *two*
    of the “three classic insoluble geometry
    problems of antiquity    ” (as they’re commonly
    known). name a constant
    disposing of the third such problem.

    this (of course) has more than one answer —
    “pi” itself would do just as well, e.g. —
    and is anyway just a trumped up version
    of mathmom’s much more natural question.
    just happens to be what i thought of
    when i tried to work out an answer
    *without* mentioning “circle” or “square”.

    jd’s “gamma of one-half” is much my favorite
    answer so far, but what should we expect?
    — it was his question!

    Reply
  10. Clueless permalink
    October 30, 2007 am31 3:21 am 3:21 am

    Integral from -Infinity to Infinity of exp(-t^2) dt

    Reply
  11. Pseudonym permalink
    October 30, 2007 am31 10:53 am 10:53 am

    JBL: Sorry, yes, you’re right.

    Reply
  12. vlorbik permalink
    October 30, 2007 pm31 5:03 pm 5:03 pm

    jbl’s correction of pseudo’s example, i mean.
    why look it up when you can just cite sources
    completely at random? anyway, clueless’s #10
    is topping the chart (& is unlikely to be beaten).

    Reply
  13. Clueless permalink
    October 30, 2007 pm31 6:50 pm 6:50 pm

    Actually, by using symmetry and by using a substitution of x=t^2, the integral reduces to the definition of Gamma(1/2).

    Reply
  14. v permalink
    October 30, 2007 pm31 9:08 pm 9:08 pm

    granted; still more elegant because
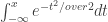
    *much* more familiar … a vast army
    of undergraduate students “learn” about
    \int_{-\infty}^{x} e^{{-t^2}/over2} dt
    in statistics classes, whereas it’s possible
    to get a math doctorate knowing little more
    about gamma then gamma(n) = (n-1)!
    (for n a natural #).

    Reply
  15. jd2718 permalink*
    October 30, 2007 pm31 11:53 pm 11:53 pm

    You are all winners with this one. Have to try it again sometime, it’s been fun.

    Reply
  16. Clueless permalink
    October 31, 2007 am31 2:40 am 2:40 am

    Interestingly, if you write the equation as

    Integral from -Infinity to Infinity of (exp(i^2x^2)) dx – sqrt(pi)=0,

    you have an alternative to Euler’s equation that does not have unity, but does have infinity and the indefinite variable.

    Reply
  17. w permalink
    November 1, 2007 am30 7:47 am 7:47 am

    that is so funny – a student asked me that exact square root today!

    Reply

Leave a reply to Clueless Cancel reply