Puzzle: Probability. Bitstrings.
October 26, 2007 pm31 11:23 pm
Here’s one I haven’t answered: Given a random bitstring of length n, what is the probability that the longest string of 1’s is the same length as the longest string of 0s?
11111001000100101011111011011000001
Let’s explain a bit (ha ha). A bitstring is a “word” made up of 1s and 0s. The bitstrings of length 2 are: 00, 01, 10, and 11. The bitstrings of length 3 are: 000, 001, 010, 011, 100, 101, 110, and 111. In general, there are 
- So, when n = 2 we have 4 bitstrings, and 2 of them (01 and 10) have longest strings of 0s and 1s of equal length. (probability is 2/4)
- When n = 3 we have 8 bitstrings, and 2 of them (010 and 101) have longest strings of 0s and 1s of equal length. (probability is 2/8)
- When n = 4, we have 16 bitstrings, and of them (0011, 0101, 1010, and 1100) have longest strings of equal length. (4/16)
And after that, it looks like it gets complicated. Can you answer for the next few numbers? Can you generalize for n? And do the answers for even n‘s and odd n’s behave differently?
JD2718 
I counted the number of bit strings with this property, for each length from 0 to 20, and I found the following values.
1, 0, 2, 2, 4, 6, 14, 26, 54, 106, 210, 412, 812, 1596, 3150, 6226, 12338, 24496, 48720, 97020, 193396.
I could not find this sequence in the Encyclopedia of Integer Sequences, even with “superseeker”.
I have posted Python code at http://pastebin.org/6119
Thanks for that. It looks a bit
ish, but not quite. We’re converging towards something, maybe?, but sometimes a number is just a number.
As I (hand – ugh) counted the first few, it occurred to me that this might be ugly. On the other hand, if n is even, and the number of 1s and 0s are equal… still ugly. I’m wondering if there are any nicely behaved sub-problems here.
Btw, David, please excuse me for not soliciting you for the last Carnival of Mathematics. But it looks like you have stopped updating?
I started this one last night (by hand) and agree it is not pretty. As quarter grades are due and I have to get ready for parent conferences, hopefully I’ll be able to get back to this one soon.
Great problem though.
A string of consecutive 1’s or 0’s is called a run. Run-length encoding, wherein the lengths of the strings of consecutive 0’s and 1’s are alternately sent is the basis of fax transmission.
Is there a tradition of puzzle/problems in this area? It seems like a good place to play.
Or are there sets of well-known (but not to me) problems?
I just figure that every area of math with serious practical application ought to give rise to some nice recreational math as well.
So, I also agree that this question doesn’t obviously have a nice solution, but let me offer some problems with the same flavor. Although David Radcliffe started his count at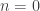
, in several of these it is an outlier that should be ignored (i.e., start your count at 
).
1) How many bit strings are there so that the longest run (of both 1s and 0s) is of length 1?
2) How many bit strings are there so that the longest run (of both 1s and 0s) is of length at most 2?
3) How many bit strings are there so that the longest run of 1s is of length 1 but the longest run of 0s can be any length?
4) How many bit strings are there so that the longest run of 1s is of length 1 and the longest run of 0s is of length at most 2?
5) How many bit strings are there so that the longest run of 1s is equal to the longest run of 2s and both are equal to 2?
A related subject is ascents and descents in a permutation. I.e., given the permutation 42351, we can keep track of its “shape” by the bit string 0110, since it first has a descent (4 > 2) then two ascents (2 < 3 < 5) and then another descent (5 greater than 1). In this way, we can map every permutation of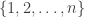
to a bit string of length 
. (I think usually one uses a and b instead of 1 and 0, and this is called the ab-index of the permutation, but whatever). Note that the same bit string can be assigned to several permutations, i.e. 31452 also has associated string 0110. There are lots of questions related to this, some of them quite hard. Here are a couple:
1) Of all bit strings of length
, which ones are associated to the smallest number of permutations? (Easy) The largest number of permutations? (Not easy)
2) How many permutations are associated to bit strings with exactly
0s? (There is a nice recursion — these numbers are called Eulerian numbers, and then pop up in a variety of interesting places.)
Ok, so for 123 we have:
123 aa
132 ab
213 ba
231 ab
312 ba
321 bb
And it gets more interesting for larger n? Do I have it right? Are your questions 1) and 2) at the end of your comment well within my range, or over my head (or right on the line, which would make me happiest)?
Yes, that’s right. The first part of (the second) question 1 should be well within your range. Finding the recursion in question 2 should also be doable, although harder. The second part of the first problem is out of your range (it requires a little heavy machinery regarding the ab-index).
Also, thanks for fixing up my comments.
“1) How many bit strings are there so that the longest run (of both 1s and 0s) is of length 1?”
Easy
“2) How many bit strings are there so that the longest run (of both 1s and 0s) is of length at most 2?”
Proud of myself here. It took all of about 15 seconds to rephrase this into a familiar problem. 466 when n = 13, right?
I’ll look at the others later.
You’ve suffered an off-by-one error: our sequence begins 2, 4, …, not 2, 2, …. Otherwise good so far, though.