I ban FOIL
We should teach factoring. But we should also make certain that the stuff we teach before factoring supports the method(s) of factoring that we will teach. Today we’ll look at multiplication of terms with like bases, and at polynomial multiplication. The next post will address the first part of how I teach students to factor.
- they multiply the bases
- they multiply the exponents
There is nothing amazing in how I deal with this:
- emphasize ‘spreading out’ the multiplication, eg
. At a certain stage they will just know the rule, but there should be no rush to that stage.
- Every student learns that eight times four is thirty-two, not sixty-four. So forget your rules? Think about this:
(FOIL/NOFOIL below the fold —>)
Multiplying polynomials
I see merit in several methods of multiplying polynomials.
My personal favorite is long multiplication. It looks just look the operation from arithmetic, with minor adjustment. Why not fall back on existing, solid knowledge? (I sometimes use this method)
Here are examples of long multiplication (arithmetic, left, and polynomial, right) from Eric Weisstein’s Wolfram’s MathWorld.
However, while my students see long multiplication, we emphasize distribution, since our method of trinomial factoring rests on reversing the distribution process. The intermediate steps in multiplying by distributing will also be the intermediate steps we encounter in factoring.
Binomial times binomial: 
Applying the distributive property to polynomials may be a bit novel, but kids don’t find it particularly challenging.
So, why, oh why, does so much of this country teach a mnemonic for multiplying binomial times binomial? and not touch long multiplication or distribution?
This is FOIL for (x – 8)(3x + 16):
F stands for First (first two terms)
O stands for Outer (outer two terms)
I stands for Inner (inner two terms)
L stands for Last (last two terms)
And then O and I need to be combined.
Look, I’m all for kids remembering things, and if a mnemonic helps, great. But here? No way! FOIL only works for binomials, a subset (albeit very important) of polynomial multiplication. Far worse, however, we can appeal to our knowledge of arithmetic (through long multiplication) or our knowledge of fundamental properties (through multiple distribution). FOIL appeals to nothing but cutesiness.
So I ban it. And the kids who already knew it fuss. And I explain why we don’t use it. And the kids who never knew it are curious how it goes, watch their friends do it, and decide to stay away. After a week I still have one or two grumbling at me under their breath, but they can handle other methods.
And a month or so later, when we begin factoring, the heavy emphasis on distribution pays off.
Trackbacks
- Welcome to The 134th Carnival of Education at www.matthewktabor.com : Education and School Issues, News and Analysis
- Carnival of Education v. 134 « Casting Out Nines
- Trinomial Factoring - nice site and last detail « JD2718
- Puzzle: Factoring Trinomials « Let’s Play Math!
- Misdirection in Algebra « JD2718
- Put The FOIL In The Recycle Bin, Please | The Jose Vilson
- sciencestage
JD2718 
Thank you.
When I learned FOIL the first time I got very confused: I had thought that multiplying polynomials was pretty simple, but if it needed a new rule and acronym I figured I was missing something.
If the kids get distribution, they don’t need FOIL. If they can use FOIL, they still need distribution. I think your ban is worth the fuss.
I agree. I’ve only mentioned FOIL because other teachers will expect that they’ll have heard of the term, but it’s all distribution and I don’t like special-cases.
Just experienced this with my seniors during the Algebra Review. Most were fine multiplying binomials, but anything else…ARGH!! Startup problems will consist of distribution for a few days. Thanks for the refresher as to other methods.
I think the worst thing about FOIL (and I had to think a bit too figure out what it meant) is that, by separating “inner” and “outer” from “first” and “last,” it actually de-emphasizes the pattern of what you need to do.
— Rachel
I don’t use “FOIL” either. I find the kids remember the word, but not how to use it. I also avoic CPCTC when I teach geometry–same reason.
When I teach geometry, I try to get mostly if…then statements out of the kiddies. No matter how badly they abbreviate them, they carry meaning.
CPCTC, though, kids remember the sound and throw it in anywhere. I’ve seen ‘stopped clock’ proofs where it was used for more than half the reasons.
Contrast? Here’s what I allow: “if 2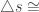
then corr sides 
”
(or angles. But I prefer they specify)
I’ve pretty much taken your approach for several years now. Thanks for the post.
I hated FOIL when I learned it too—it seemed so superfluous to have a special case of a basic pattern.
Well written article!
High schoolers and lower-year university math students seem to think mathematics is all about memorizing formulas and stupid mnemonics while completely not seeing and understanding the beauty of efficiency and generalization as shown in this post.
FOIL is used to multiply binomials, not for factoring! I’m off to leave them a comment…
FOIL was handy because you had (usually) the two terms that needed to be canceled right next to each other; your 16x and -24x are hard to miss.
That said, distribution is better.
FOIL is horrible . . . not only is it binomial-specific, but it also suggests that the order of multiplication of terms is important, when, of course, it isn’t. Give me a nice left-right distributive property rule that works in all cases, and make mathematical rather than mnemonic sense, and I’m a happy boy.
Now if we could just get rid of those damn “X”‘s the kids use for factoring.
Dan
Someone out there has to like it, or I wouldn’t get kids every year who come in knowing it from middle school.
Thanks for pointing out what aspect bothers each of you most.
And sailorman, in long multiplication the two terms to cancel are immediately over each other, addition style. And in double distribution they end up immediately next to each other. FOIL offers no advantage there.
“Why not fall back on existing, solid knowledge?”
Wow – do your students know how to do long multiplication? I’m impressed. Most of ours can’t even do the product of single digits without a calculator. The lack of “number sense” is a big concern of mine. How can you do algebra if you are not even sure how it works in number?
I agree with your FOIL ban.
Most of my students can multiply. Some, though, come from a district where they learn very well what multiplication means, can explain it in several ways, but don’t actually know the facts. Oooph.
Fascinating. I teach middle school and we cover the distributive property. I don’t remember how it came up, but one of my students clearly had an epiphany in that class so I challenged her to multiply a couple of binomials (not something we cover in our middle school program). She did it easily (as a side note, she was a student with an IEP) because she understood the distributive property. I was so proud of her. As I read your reasoning, that was all I could think of. If I ever do teach high school, I will remember this.
My wife, an elementary school librarian, showed me this article, as I’m in school right now to be a 2ndary math teacher. My instructors hate FOIL as well as other “tricks” like lcm (lcd) when adding fractions. I’m glad she pointed this out, as I’d already made up my mind to never use those “tricks,” and this has reinforced that notion.
@pisani – The problem is not that tricks are in use, it’s that they are sometimes the ONLY thing in use! I think it’s neat to point out patterns, but only AFTER the theory is understood. Since there’s usually not time for both, you’ll find that teachers tend to do one or the other.
I hardly consider FOIL a “trick” though, because it’s limited to one specific case. And believe me, it takes just as long to “teach” them FOIL as it does to teach “distributive multiplying” so why bother?
I see how you teach it now! Interesting. I agree with you that “FOIL” only takes care of a factored trinomial where there’s no “inner”. Give a FOIL kid a binomial/trinomial multiplication problem and they don’t know what to do with the trinomial’s middle term!
p.s. I’m teaching a number theory class to 10th graders next year and plan to have them informally prove that your method of distribution gives the same answer as after foiling. Cool stuff. Thank you.
I do wonder still WHY we can distribute pieces of the first polynomial to the second polynomial. It’s easy enough to see why we’re allowed to distribut the 3 in 3(x + 2) because there are 3 “(x+2)”‘s so distribution is easier than adding (x+2) + (x+2) + (x+2). Multiplication is a quicker way to add.
But as for a polynomial multiplied to a polynomial… what allwos us to do this?
The more math I learn the more confused I get (myself)!!
I still like foil for a couple of reasons..I think one of the things that we need to constantly develop is mental math. Doing the “I” and the “O” mentally is an important step in the development of math skills. If kids are working on a long problem in an upper level class that involves bi times bi, and then they use the box method (e.g), I would be very concerned.
The second reason, to use the tool analogy I have seen, is it is a special tool for a special example…but I say, what a special tool it is!. If there is a special tool that can be used that would make