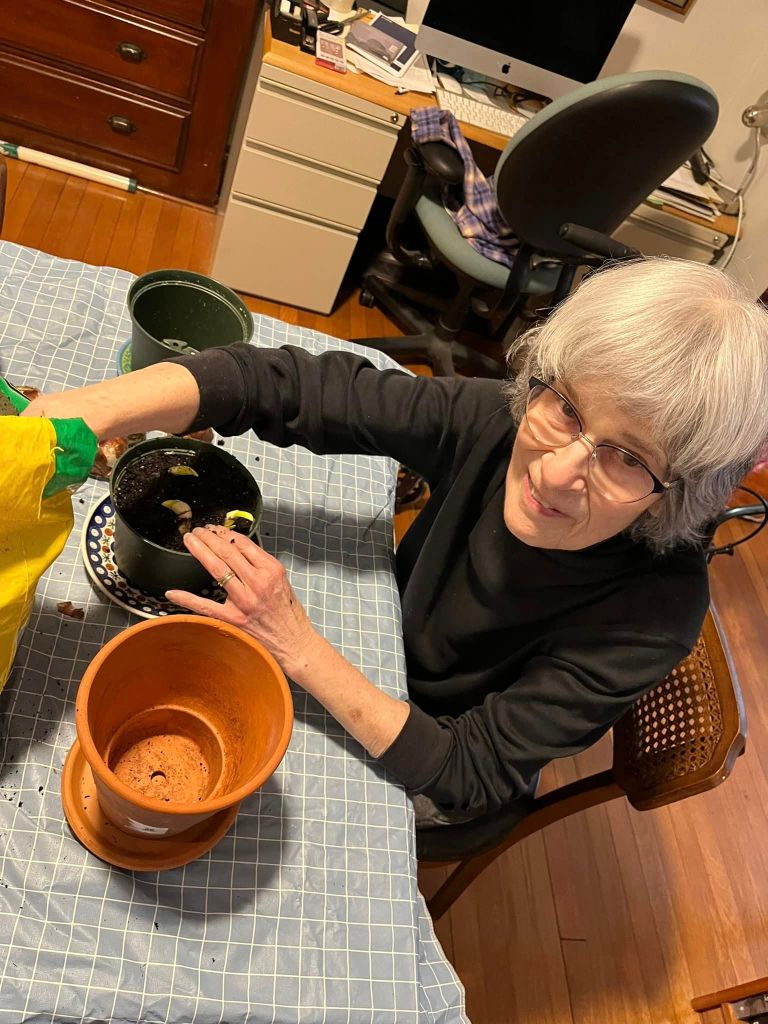UFT Welfare Fund nest egg – bigger than most nests
A nest egg. A rainy day fund. A reserve. Back up. We all have some, or would like some. In case things go sideways, a way to pay some bills in the meantime.
If you have assets that would cover a full year of expenses, that’s pretty good. And in 2011, the United Federation of Teachers Welfare Fund was about two-thirds of the way there: they had assets of $239 million, and expenses of $306 million. They also had revenue of $289 million. That means they lost a little, and the nest egg went down to $222 million.
As long as revenue and expenses were balanced, the assets (the rainy day fund, the nest egg, the reserve) stayed in that range. At the end of 2011 $222 million.
| Year | Assets |
| 2011 | $222 million |
| 2012 | $227 million |
| 2013 | $252 million |
| 2014 | $258 million |
| 2015 | $268 million |
Stable. Expenses surprisingly did not go up ($306 mil in 2011, $300 mil in 2015). This makes sense, right? I mean, to the extent that chunks of cash large enough to pay Donald Trump’s bond make sense. I don’t know about you, but I have trouble grasping just how much these numbers are. But however big they are – expenses not rising, revenue not rising, assets not rising, or just rising a little, that would seem to fit.
But look what happens next:
| Year | Assets |
| 2016 | $303 million |
| 2017 | $350 million |
| 2018 | $434 million |
| 2019 | $523 million |
| 2020 | $634 million |
| 2021 | $752 million |
| 2022 | $800 million |
What the?
Every year since 2016 the UFT Welfare Fund has taken in much more money than it has spent. Assets are doubling in 4-6 years? Wow.
Today, no answers. Just wow.
Revenue mostly comes from the City giving the Welfare Fund money, that the Welfare Fund then spends on administrative costs, and on us. Or, apparently, doesn’t spend. Those are some pretty hefty crumbs leftover.
Maybe 2014 was an inflection point. Maybe these huge increases have to do with the deal – when Mulgrew snuck into the contract provisions to cut health care (they call them health care “savings” – they save, we pay)
We should dig into more reports. Can you imagine putting fifty mil in the bank each year? And think about this. The Welfare Fund is saving money. Somehow. How?
Could it be that the eyeglass and ophthalmological reimbursements could be higher? Would that cut into the Welfare Fund eight hundred million?
Could it be that our dental plan, pretty lousy for a NYC union, is a discount plan – and that a plan like DC37s or the PSCs (note to self, let’s check other dental plans) would cut into that 9-digit UFTWF bankroll?
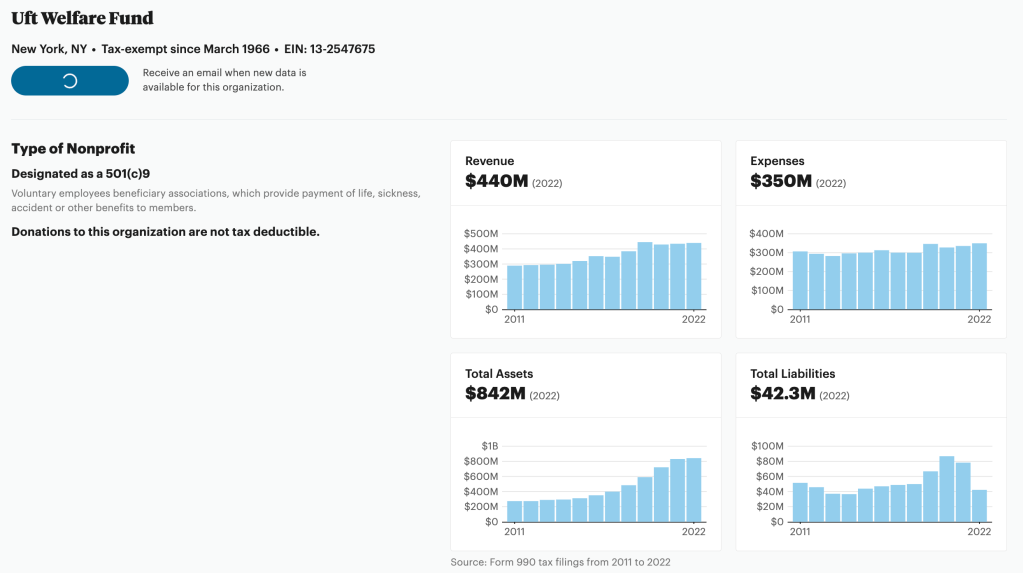
Look – I have a few questions now – no real answers. But before Mulgrew gets control of a cool billion, maybe we should dig into this. Maybe the Welfare Fund should be spending more money on, well, something worthwhile. Like our members’ welfare.
The Company You Keep
At the hearing last Thursday… (oh there’s a lot to write, but I won’t)… the UFT’s lawyer was there… Alan Klinger… sitting with… the lawyers for the City… sitting with those who are trying to force retirees into Medicare Advantage. And doing it on our dime.
The United Federation of Teachers’ lawyer sat with the City attorneys and helped shape arguments that, if they succeed, will force retirees out of traditional Medicare.
Just another reminder…
60
I turned 60 a month ago. Made me smile.
I used the day and the days immediately before and after to celebrate. Not sure what I was celebrating, in particular, but celebration seemed in order. When the odometer rolls over, there is a sense of excitement, but the world hasn’t changed. Maybe it’s just a moment to reflect.
Friday before my birthday I went to the bar – and was joined by friends, former colleagues, former students, family. Hours passed, chatting, relaxing. I felt good. I wore my brand new “60” t-shirt. Someone brought me home-made chicken soup.
And my birthday day? I met ten people at Van Cortlandt Park. And we walked through the park and through the woods and by the golf course and around the pond. Three or four miles of walking and chatting and most of them did not know each other so meeting new people. It was gorgeous weather and I had a great time. I should do this again next year.
Afterwards some people went home, but half of us made our way to Com Tam Ninh Kieu, and I had birthday pho.
So the idea, instead of the big party with gifts and cake and all the other sort of formal stuff, instead of that, going somewhere comfortable, being surrounded by friends, and doing something relaxing – I like that. It worked. I’ll do it again.
Which brings me to my New Years resolution #10 – Have a Good Birthday. I accomplished that one.
What about the other resolutions?
#3, #8, No Progress: No zoos so far. No ferries so far. But with warmer weather.
#6 – flowers in the apartment. I have had some every day this year. Today there are three amaryllis in bloom.
#1, #4, #7 – Tracking stuff – I’m solid. Logging the books I am reading, the hikes I am taking, and recording vitals. Does it help me read more? I think so. Hike more… not really, but it might in the future. Pay more attention to my health? Not sure, but it doesn’t hurt.
#2 – say yes to more social invites. I forgot I made this one. I’m not sure. Birthday energy soaked up a lot of my social time, so it’s hard to say how I’m doing. But I did have birthday outings, beyond the two I wrote about here. And they all involved food, drink, walking/hiking, or some combination.
#5 – politics – speak the truth, work for change – yup – involved. Working for a ceasefire. Working on the campaign to take back the Retired Teachers Chapter (and preserve medicare).
#9 – do not download games to my phone? Phone’s clean. Not a one. But it feels like going through withdrawal.
#10 – Have a good birthday. Yup! Yup! Yup!
2718’s 2024 Resolutions
- Log my hikes. I won’t resolve to hike more (even though I mean to). I will resolve to record them though, in my “Hike Book” – a black and white cover bound composition book.
- Say yes to more social invites. I was out last weekend – at the sort of thing I usually miss – and it felt good.
- Visit all the NYC zoos. And the Aquarium.
- Log my books. I won’t resolve to read more – see above – but I am recording my reading, whether a whole book or part of a chapter, in my “Book Book” – a black and white cover bound composition book.
- Reread my advice to myself. I think kids asked for advice for a yearbook quote. And this is what I came up with, here: “Speak the truth. Work for Change. It’s not about you.” And expanded here: “Act against racism. Act against anti-immigrant bigotry/hatred. Act against sexism. Act against homophobia. Act for fairness. Act in solidarity. Looking away = acquiescence (and is absolutely unacceptable)” Figure this will drive what I do/say about Gaza, and about preserving medicare.
- Keep flowers in my apartment. I may grow some. I may buy some. I may buy plants that flower periodically. But this is easy, and flowers make me happy.
- Track my vitals. Won’t promise to lose weight or get more fit. But I resolve to pay attention.
- Ride as many of the NYC ferry lines as I can. Even Rockaway.
- Do not download games to my phone. I deleted all of them, one at a time, last summer and fall. I miss them – but like withdrawal – not like nostalgia. My screen time dropped immediately. Stay the course. Solid resolution.
- Have a good birthday! I needed one resolution that felt like a resolution. And three score is a lot. I should have a day or two to smile about it!
New York City’s Hidden History – Freedom Day
Huge civil rights protest, half a million, 60 years ago. And some of you might want to say, “but the March on Washington was sixty and a half years ago – and it was a quarter million” – which is correct. And it makes the point. A protest, twice the size, not in Washington DC but here in New York City, happened 60 years ago, and it is hidden.
The NY Daily news sent a note to subscribers – 60 years ago (Wednesday) a few hundred school kids skipped schools to greet the Beatles at JFK. A few hundred. None of the NY newspapers sent out notices about the 60th anniversary of half a million kids boycotting school earlier the same week.
Why hide the history? Few people know about “Freedom Day” – it is omitted from our history text books – around the country, and, worse, in New York State and New York City. Why do leaders and educators hide such a major event?
Let’s pause for a second, and just review what happened. February 3, 1964 was Freedom Day in New York City. 470,000 students boycotted school, and many engaged in additional protest and demonstration. They were demanding integration. They got empty promises, that were broken.
I don’t trust you anymore
https://www.youtube.com/watch?v=LJ25-U3jNWM
You keep on saying, “Go slow”
Go slow
But that’s just the trouble (too slow)
Desegregation (too slow)
Mass participation (too slow)
Other actions, strategies, and protests have occurred since. With the same results. Or less. New York City operates one of the most highly segregated big city school systems in the nation today.
From Time Magazine, September 2020:
(that’s an 8 minute video. There’s also a print story)
So Freedom Day was momentously huge. It did not bring about change. It set the pattern for promising discussions or studies down the road, and delivering nothing.
Is Freedom Day part of our history?
If a textbook in Colorado skipped over a huge protest in another part of the country that did not result in big change – I kind of get that. But half a million students is a lot. And the fact that the Civil Rights Movement produced the March on Washington that we think of as a turning point, but Freedom Day, twice as big, that did not change anything… probably worth mentioning.
But we are not in Colorado. We are in New York City. And when there are large national events or changes, we often include lessons on how they played out in our state. New York City during the Civil War (draft riots). New York City and immigration (Jacob Riis and Tenements). New York City and suburbanization (Levittown). But what about the struggle against segregation? That was across the country, including here. And a massive school boycott – that’s the biggest political action by students in New York City, well, ever. How do we leave our history out of our textbooks?
There is Black History in New York in our textbooks. I don’t have a DoE approved book at home – but Brittanica Kids has an article about riots in Harlem. But nothing about Freedom Day. Freedom Day was organized. It involved many, many more people. Why would Brittanica (and I assume other texts) privilege a story of chaotic response over an inspiring, bigger story of well-organized response?
Is Freedom Day “uncomfortable”?
If the March on Washington is history, but Freedom Day is not… If the Harlem riots are history… but Freedom Day is not… maybe the question is who is making that decision – and do they have an interest in including some stories and excluding others.
Yet, King highlighted the venality of more “polite” forms of racism and challenged Northern liberals to address racism at home — and not just in the South. Violence and hate-filled rhetoric were not the only methods by which White supremacy was maintained. King identified how people, including those who may have deplored Southern injustice, maintained the racial status quo. Moderates and liberals deployed “both-sidesism,” argued that time would solve the problems of racism, cast disruptive protest as unwise and unreasonable and embraced ideas like the “culture of poverty” to justify strong-arm policing and explain away inequities in their own cities.
https://www.aaihs.org/martin-luther-king-jr-s-challenge-to-his-liberal-allies/
Freedom Day challenged – and the fact that it occurred challenges – present tense – the racial status quo in New York City. The stories of the riots provide a rationale (false) for more and more aggressive policing – and that is “policing” which was, and continues to be, largely directed at people of color. And the story of the defeat of Freedom Day highlights the duplicity of those who counsel patience, going slow, “this is not the right time,” more study, etc.
More Links
I have been writing about Freedom Day for several years. This year I am four days late. Short post. Meandering story I told kids one year.
Chris Bonastia’s book covers much of the story of Freedom Day in detail. I recommend it.
Who decides what is history?
Freedom Day is uncomfortable. It is inconvenient. But it was a huge, huge event. It was defeated by double-talking politicians. And it continues to be mistreated, by being kept hidden from generations of students. Who has decided, up to now, that it is not taught in our schools? And who will decide to remedy that injustice?
Does your dog bite?
This is a post about questions that do harm, but do not make sense.
Does your dog bite? Really? No. Here’s my question.
“Can you help me find my bicycle?” “I don’t know, what does it look like?” “I don’t know. I don’t have one.”
See, the question doesn’t make sense. That was my turn. Now it’s The New York Times’ turn. Perhaps they want to talk about “learning loss” – they do that a lot. “Our students suffer learning loss” – says the Times, whose staff’s children are presumably not part of ‘our students’. “What did they learn and then ‘lose’ or forget?”
You know why there’s no answer? Because the question doesn’t make sense. Because the claim makes no sense. It would be easy to call the Times ignorant, but no. They know that “learning loss” is an artifact of ignoring students (who do learn) and instead looking at standardized test scores. They keep harping on “learning loss” because it fits their narrative.
And I’m not going to make the case here – but for The New York Times, pushing a preferred narrative is their primary purpose. They pretend to cover news as a cover. WMD. Learning Loss. Anti-progressivism. This is the publishing arm of an unpopular political current.
Today they had a different line: “children are still behind.” Behind what? They don’t say. “The students are nowhere close to being fully caught up.” Caught up to what? They don’t say. “In math, students have made up about a third of what they lost.” What did they ‘lose’? The Times does not say. They can’t say. There is no answer. They are hoping you don’t ask the question.
What happened
The pandemic came. Schools shut down. There was a really badly thought out plan to keep schools “open” even while they couldn’t be. Schools did something, students did something, but it wasn’t close to ‘normal’ school. Students’ educations were interrupted – some completely, some partially.
Interrupted Education
Education is interrupted for many reasons. Sometimes a family moves, and in that move school attendance is disrupted. Sometimes there is a crisis in a family, and school attendance takes a back seat. In circumstances like that, decisions are made on a case by case basis – give the student extra support to “catch up to where she/he otherwise would be” or let the student repeat learning the content that was missed.
But sometimes there are bigger disruption, bigger interruptions. War, famine – what does The New York Times say about ‘learning loss’ in Gaza? Child labor. Forced migration. What do societies do when education is interrupted, and then can restart? They pick up kids where they left off.
The pick up kids where they left off.
When a child transfers into our school system from another state or another country, we do not choose their courses (at least in high school) simply based on their age. We look at what they have already studied, and mastered, and what they have not studied. And we schedule them appropriately.
What should have happened
When schools came back, functioning almost normally, we had an opportunity. We could have assessed, and adjusted curricula to start where students were. We could have, we should have, scheduled students appropriately.
But that was not what happened.
What was the response
Sadly, educators’ voices were marginalized. Non-educators, who the Times speaks for, held sway. Our union, who should have been speaking for the rights of our students and teachers, instead pushed the myth that our schools had been open, and were fine. “New York City” boasted Mulgrew “kept our schools open.” If he’s boasting that our schools were open, he’s not so likely to talk about appropriate curriculum for students whose educations were interrupted. Because if education was interrupted, that would mean schools had not been really ‘open’. He could stick to his false narrative, or he could help students and teachers. He liked the narrative.
The children and their needs were marginalized. High stakes testing was centered. And each child was dropped into the course they would have been placed in had we not just suffered through a pandemic. This was cruel. This was frustrating. And this was totally unnecessary.
And my response
When a child has needs, and the system does not adjust to meet those needs, the child has not failed the system.
The system (think Department of Education. think the New York Times) has failed our children.
And no, my dog does not bite.
But you know…
No Battle for Second Place
After wasting tens of millions of dollars, Ron DeSantis dropped out the day before New Hampshire. He didn’t contest a single primary (Iowa was caucuses). Republicans have run some pretty awful campaigns. Chris Christie. Rudy Giuliani. Rick Santorum. Greg Abbott. Chris Christie. But DeSantis may be the worst.
Is that me, kicking the smug vile torturer when he’s crawling away? Nope – look here:
So sad for me. I was creating maps. Also rans. Who would be the big loser to Trump. My maps were showing who was in second. I just started last week, not anticipating DeSantis’ slimy early exit. Look here:
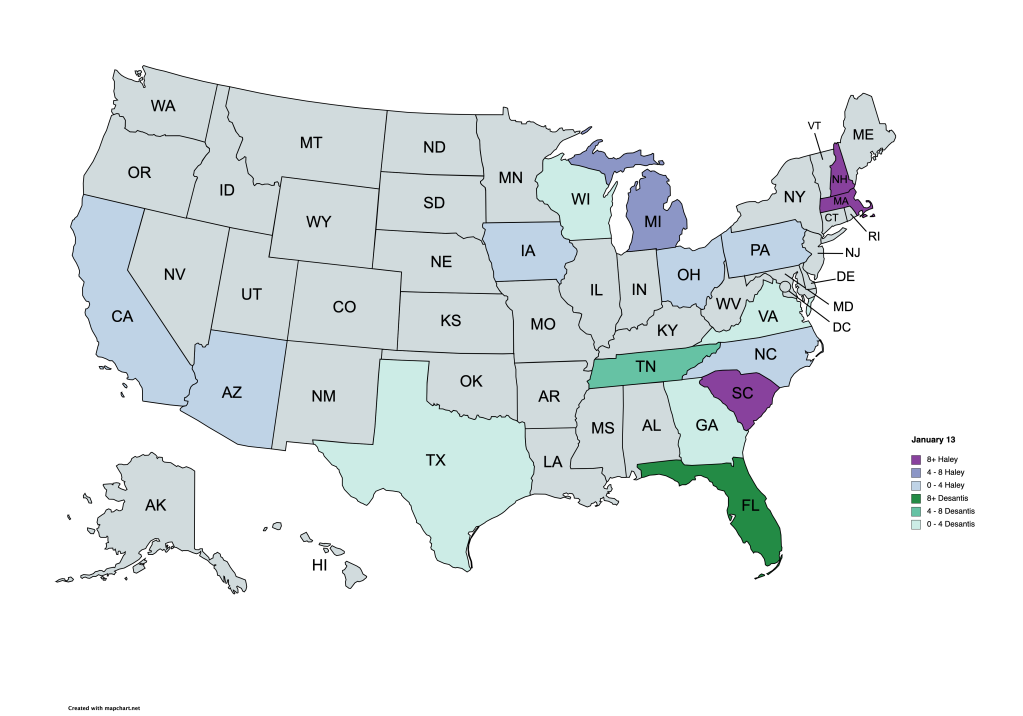
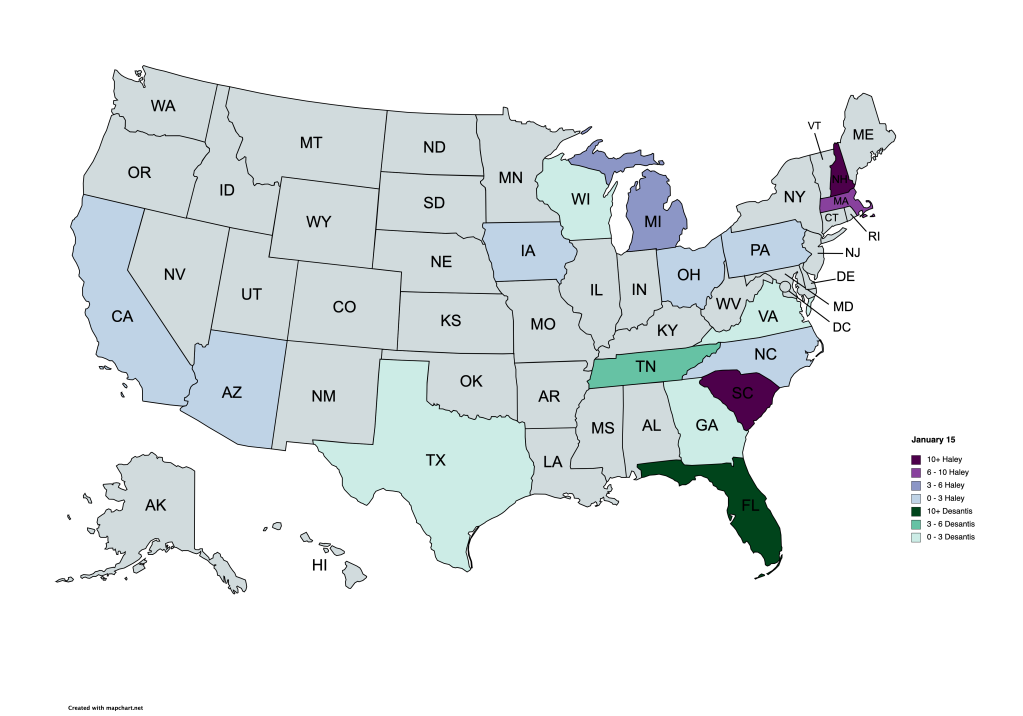
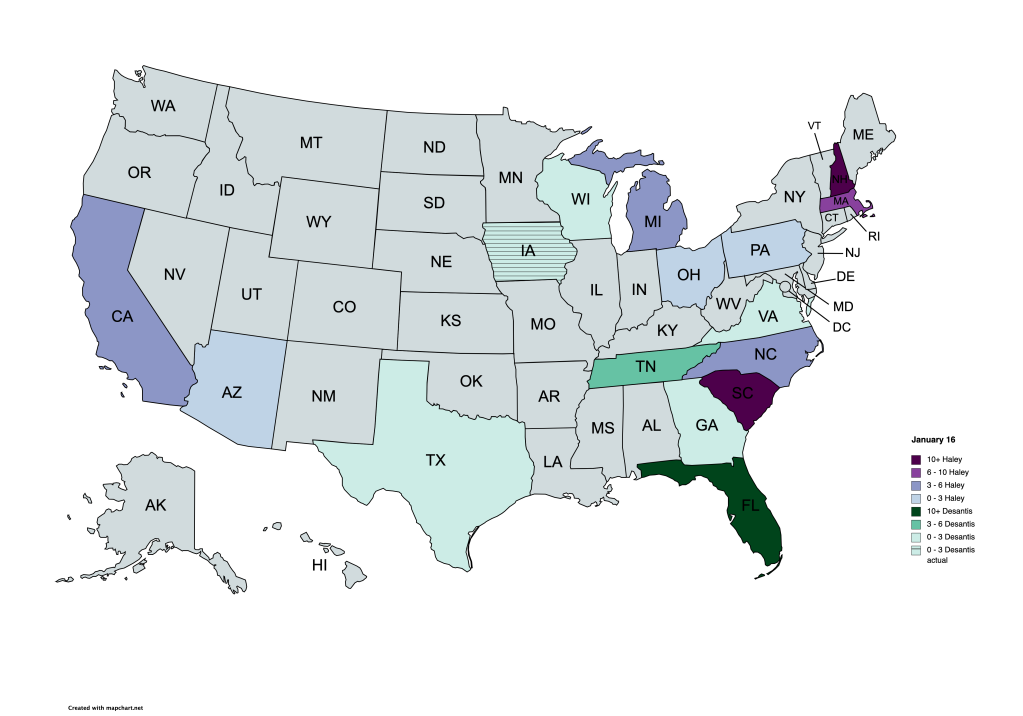
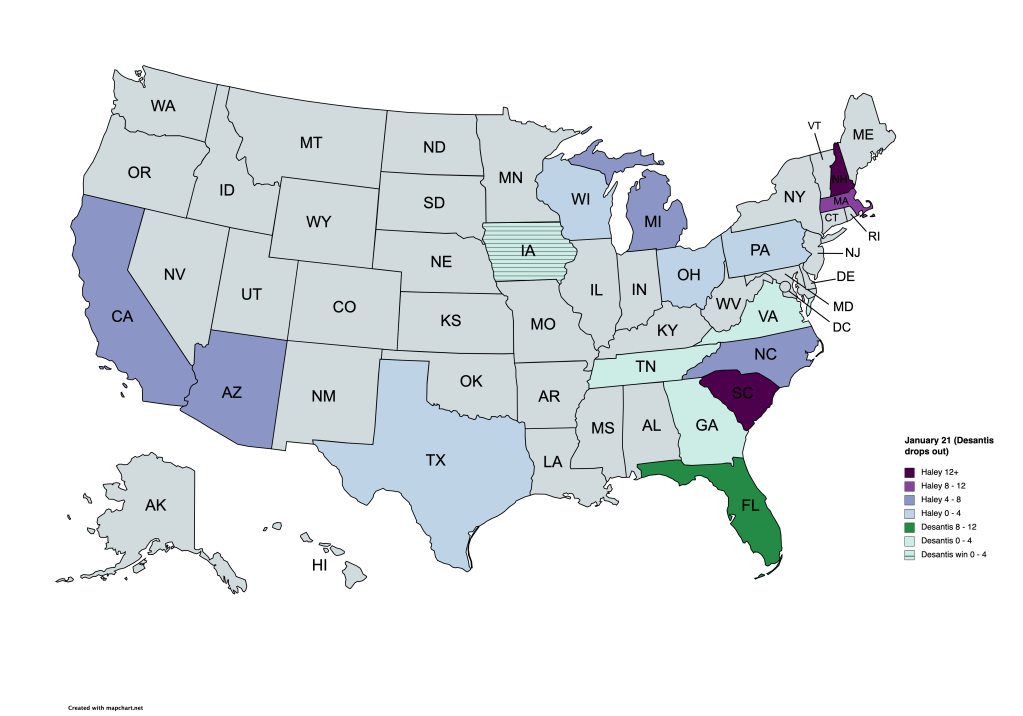
Oh well. That was just a time sink anyhow. Neither DeSantis nor Haley stood a chance against Trump. The Republican base has revolted, and is no longer loyal to its traditional leaders. White shoe, corporate, board of directors, golf meetings… they are still there… but they do not command the loyalty, and certainly not the votes within the GOP.
I guess DeSantis had an angle – Trump’s politics, without Trump. But the rank and file LIKE Trump. They like his obnoxiousness. They like when he’s a jerk. Someone wants to be Donald Trump without being an asshole? Why would anyone pay that person any attention? Why? Why Ron? (and just an asterisk, that “without being an asshole” is a stretch). So off he goes, just like a Burmese Python (in the sense of, sorry Florida, he’s yours.) And while he went without a whimper, he’s not running for vice president, so we (except for Floridians) won’t see him again.
Haley is left standing, but has no angle. She appeals to those corporate Republicans who have been removed from power – in other words – to no one who is going to make a difference. She’s got a chance to win New Hampshire (but Trump probably wins 60-40) and a long shot to take her home state of South Carolina, but that’s pretty much it.
There is a huge question mark left. What if one of Trump’s trials goes badly for him? So, yeah, I don’t know what happens then.
There’s a smaller question mark, too. Haley looks like she might be campaigning for vice president. Unfortunately, she is somewhat intelligent, and somewhat capable – baggage that Elise Stefanik just does not have to carry. Plus, can you imagine Haley doing this:
Nolo contendere!
Days are getting longer – are the weeks?
The calendar works that way. The shortest day is around December 21. And the length of the day then changes slowly. The days get longer and longer and longer, and the changes happen faster and faster. And the fastest change happens around March 21.
We are now a third of the way from December 21 to March 21 (roughly), so the days are starting to get noticeably longer.
The story continues. After the first day of spring (roughly) the days keep getting longer, but the changes become smaller, until they reach their longest (and stop getting longer!) around June 21. And then shorter and shorter, fastest change around September 21, until the cycle completes just before Christmas.
But are the weeks getting longer? This one seemed packed.
- Culture. I signed a petition to reinstate Samia Halaby’s retrospective show at the University of Indiana, which the university administration had canceled with a flimsy excuse – actually because Samia is outspoken about Palestine. Here’s the petition. Here’s an interview with Amy Goodman on Democracy Now. Also, I joined a Cultural Resistance march on January 13 and marched with some NYC teachers, and alongside marchers in solidarity with the Jenin Freedom Theater.
- Birthday. Mine is on my mind. Big one soon. But I went to a friend’s 60th – wanted to go – wasn’t sure what to expect – and had a great time – got there early, left late.
- More marching. 42nd street to 86th street Monday. Actually, 40 years in NYC, many years of many protests, and this was my first time passing Gracie Mansion. I didn’t actually see it though.
- Ceasefire? Another attempt to get the United Federation of Teachers (UFT) to take an immediate ceasefire position failed to get on the agenda. A resolution was raised by someone from the Educators for Palestine group (don’t know if they were a MORE member, might have been.) They pointed out that AFT President Randi Weingarten tweeted in favor of a ceasefire (clearly. She was responding/echoing an Israeli ally who was making the call.) It got 51% of the vote, but needed two-thirds to get on this month’s agenda. It is clear, though, that something big is going on. The UFT was long one of the most anti-Palestinian unions in the country. There has been a shift. MORE and E4P do not organize anywhere close to half the Delegate Assembly vote. That total reflects real change. Independent delegates must have voted to put a ceasefire on the agenda. And there’s no way to reach a total like that without quite a few of the leadership’s delegates (Unity) breaking discipline and voting to put an immediate ceasefire on the agenda. Strangely, New Action’s blog takes a seemingly anti-ceasefire stand. I will try to clarify; perhaps I misunderstand. But look – this is a big shift. It took years to move the UFT off of Shanker’s pro-Vietnam war position… but eventually we (before me, but, “we”) prevailed. There was a moment when the UFT shifted, and that was big. We are close to another such moment.
- Bigots in NYC? Yes, we have our own. There is an infestation called “PLACE” among some of our parent bodies. But this week we had Moms for Liberty – an invasive pest from Florida. They specialize in anti-trans bigotry, but have branched off into generic anti-LGBTQ, racism, and book banning. They were able to rent space at the Bohemian National Hall on the east side, which is actually owned by the Czech government. The Czech foreign ministry shamefully refused to step in and cancel the contract. In the end, the shabby group of bigots and right-wingers did speak, PLACE was prominent, but to an audience full of protesters (out of just 75 people) with 100 more protesters outside. I’m glad they were overwhelmed, but that’s not good enough. They should not have been here. Let’s make sure they do not come back.
- And ending on a high note – went to visit my mom. I brought her narcissus (paper whites), and she enjoyed potting the bulbs.
Bad Mom
Good Mom
Review and Resolutions
This was my first full year retired (officially from January 3, 2023). There was so much to do! What did I do? Not do?
Learn Math
I wanted to take courses. I tried to enroll non-matric at Queens College, but turned out I had already matriculated while on sabbatical in 2013 or 2014. So they took me as a continuing masters student. I took one course in the spring, and two in the fall. Two of the three turned out well. I’m registered for Set Theory and Theory of the Integral for the upcoming term. I didn’t mean to get a masters, but that looks like where I’m headed.
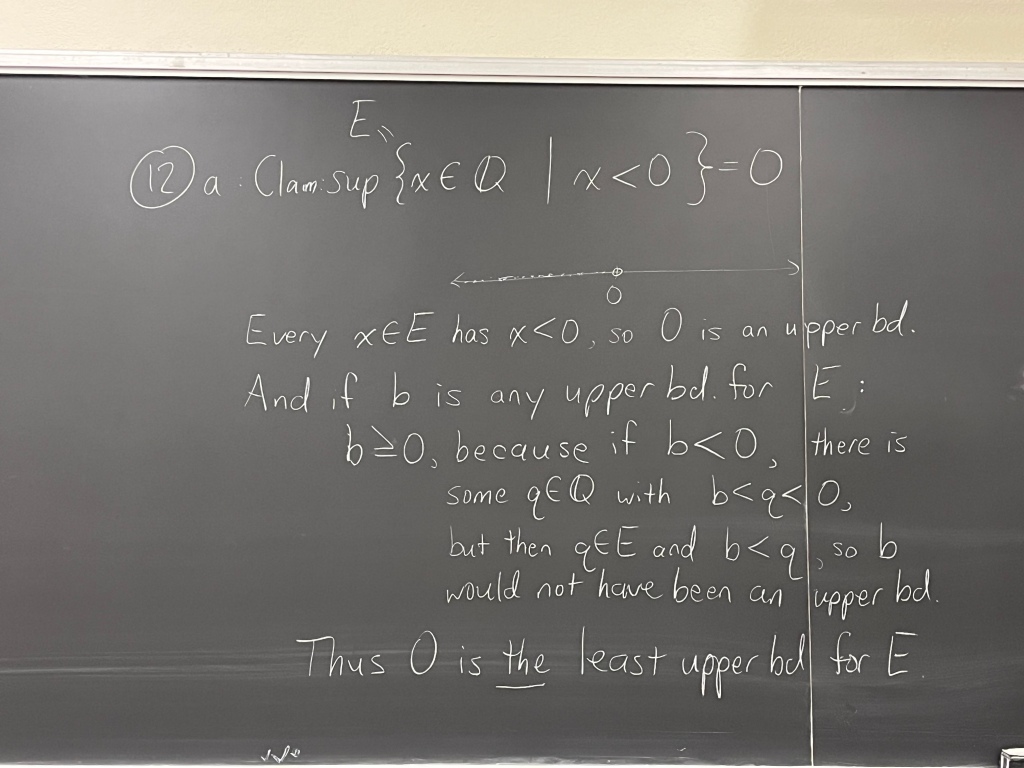
I wanted to study independently. My idea was to pick a text and read it with a group. I had some takers, in theory, but in practice I ended up working with one person, Sue, on a text that she might need to teach with. We met intermittently for a while, then drifted. But in those meetings I was reminded how much more fun it is to do math collaboratively. This is worth trying again.
Purchases
I had planned to get myself a new car as a retirement gift-to-self. But my 25 year old car runs well.
I thought about moving to a better apartment, since three houses on my block got knocked down and replaced by buildings and spoiled my view (just of Mosholu Parkway, but still. And also the roof of the library in the Botanical Garden got blocked.) But have you seen rents and prices? I’ll try to travel and go out more so I’m not spending time staring at a wall.
Travel
Where do I begin? Probably with a ticket. But I haven’t bought any. No boats. No trains. A drive upstate for Juneteenth. One plane (weekend in Chicago). Spent a week on a pond in Maine (long drive). And that’s it. Why, now that I have time, has travel been a bust? Hell if I know. I should do better.
Books
I had almost completely stopped reading towards the end of my teaching career. Figured I would jump right back in. Wrong. It’s taking work. But I did read in the fall of 2022. Got starts on a few books. Didn’t finish many. And picked up the pace very slightly this year. 90% non-fiction. Some of it is math – but I like science and history and politics. And education.
I read Clara Hemphill’s new book. And a long book about the mummies of the Tarim Basin. And a collection of essays about a boarding school for Native Americans in California. That one was tough. Something older by David Montgomery about salmon. The best part was about what rivers look like if people don’t clear them and straighten them, at least that’s what I thought. Robert Meeropol’s autobiography. Chris Bonastia’s book about New York City schools and segregation. There were a few more, but not many…
Hiking
Now this has been great. 2023 was my best walking year since before the pandemic. And 2024 is already looking better. In 2023 I spent more time in the New York Botanical Gardens (practically my neighbor – I get to the closest gate from my apartment in 6 minutes) and in Van Cortlandt Park (almost my neighbor) then, well, pretty much any year since my unemployment of June 1994 – August 1995. I have also been hiking up the Hudson. And in northern New Jersey. And a little bit in southern Connecticut. And exploring parts of Westchester and Putnam. Did you know that there’s lots of little private “preserves” that are open to the public? And some are truly lovely. Oh, and I also went on a few marches, but saving that for another section. And also a few mushroom walks. I like those. The walks. And the mushrooms.
Blogging
Hey, I kind of leveled off. Well less frequent than 2020, but much more content than the years immediately preceding the pandemic. The story, not that interesting maybe, was that I’d dwindled to a handful of posts a year, and was thinking about closing shop. And in March 2020… In any case, I’d like to write more in 2024.
There’s also a new kind of blogging, sort of. I’m putting up YouTubes with Arthur Goldstein. Kind of a video podcast. We call it “State of the Union with Arthur and Jonathan.” I think we have four episodes up, it’s been about once a month. We should regularize SotU, and put them out more often. That’s on me.
And back to this blog – a lot of cool kids have switched to Substack. Maybe I should think about that.
Joining Stuff
I joined the NY Mycological Society. I’ve been on some of their walks, and a few of their dinners. I joined the Van Cortlandt Park Alliance. I’ve been to a few events, and volunteered once. I’d do that again. Also the Bronx River Alliance. Volunteered once. I’d do that again.
Activism
It’s now been over a year working with Retiree Advocate. We have a big election coming up this spring – challenging Mulgrew and the Insurance Industry for control of the Retired Teachers Chapter. I’m doing a lot of work… I don’t think I could keep up this pace forever, but a few months… sure.
Joined the Northwest Bronx Community and Clergy Coalition. Really nice folks. They treat their supporters, well, like friends. I always feel welcome. And there is good work. I’m excited by their advocacy around the Kingsbridge Armory. Activism. That comes with food and matching t-shirts. These are good people.
Joined the Bronx Working Families Party. We will see. There’s not as much to do.
It’s been over 100 days of destruction of life, property and infrastructure in Gaza. The barbarity of the Israeli assault, fully backed by the US government, has shocked much of the world, and has opened many previously unopened eyes. Even many supporters of Israel have been stunned by the undisguised cruelty. I have done some “social media activism” which is not much, but have also been at protests in Brooklyn and Manhattan, honked greetings at protesters as far away as Hamden, Connecticut, been uptown, midtown, downtown, east side, west side, and was there when we shut down Grand Central Terminal.
I joined Jewish Voice for Peace a few years ago, and have been involved in some of their activity. I have signed onto Educators for Palestine, and marched with a few of them last week.
I used to go to lots of protests, even organized some, but I’m out of practice. I think I’ll keep at it. That’s not a resolution, it’s just what I will do. Because it is important. Because the demand for a ceasefire is completely appropriately. Because the demand is made of our government, our government which prevents a ceasefire, prolongs the bombing and killing, indirectly, and directly, with exports of weapons and ammunition.
Food
I started avoiding beef just before the start of 2023. And for some metabolic stuff, I reduced bread and pasta, a lot. I cut out desserts, almost completely. Tried to eat less fried food. No fruit juice. And absolutely zero soda (excluding seltzer). Whole grains yes – especially faro, barley, buckwheat (kasha). More vegetables. Less other red meat (with beef 99% gone). More fish. Nuts and dried fruits for snacks. Kim chi. More cooking at home. EVOO. Smaller portions.
I don’t know if I cured anything. But I feel better. People say that I look better – and I should choose to believe them! (one person, I thought they were hitting on me. And after embarrassing myself I learned, nope, that wasn’t it, they just thought I looked better. I should have believed them!) Blood pressure is better. Doctor warned me not to go too hard, so I’m easing up. But some of these adjustments are sticking.
Teaching Math
I worked at a math summer day camp for rising 7th graders. And I did Saturday enrichment with 8th – 12th graders this fall. I like this. Low stakes. Interesting material. No test prep. I’ll keep doing this work. It’s exactly what I wanted to do. I’m going to try working with student teachers this spring – I’ll see. It could be cool. But the work with kids could turn out to be enough.
Being a Tourist
So I’m in New York, a world class city, and I have time… more time than I did when I was working full-time. So, I reasoned, I want to go out and be a tourist. Museums. Restaurants. Sights. Ferry rides. All of it. And… I did a little… but very little.
With my IDNYC (New York City ID) I can get free one year non-free-renewable memberships to a bunch of things. So instead of trying a bunch of different things, I signed up for a one-year membership to the Wildlife Conservation Society. That covers the Bronx Zoo. Queens Zoo. Central Park Zoo. Prospect Park Zoo. And the New York Aquarium.
Resolutions
A resolution should be something that 1) I can do and 2) I really have control over and 3) whose success matters to me and 4) that I can reasonably achieve. There are a lot of things I want to do, or to do more of, or to do better. But most of them make lousy resolutions. I don’t necessarily have good control over them. Or they are things that are good ideas, but I know they are difficult for me. Sometimes I know what I want myself to do, but have trouble making myself do those things.
It would be easy to resolve to read more, travel more, eat less and better, start a math book club, hike more, lose weight, blog more, make more “State of the Union” episodes, and visit more cool things in New York. But as well-meaning as each of those resolutions are, I don’t think making them is meaningful, not when we know in advance that good intentions might not play out. Resolve not to be late anymore? Well, I would like that, but I know this is very difficult for me. It’s not just about trying harder. Instead, here are my resolutions – doable, and pleasing – for 2023:
- Log my hikes. I won’t resolve to hike more (even though I mean to). I will resolve to record them though, in my “Hike Book” – a black and white cover bound composition book.
- Say yes to more social invites. I was out last weekend – at the sort of thing I usually miss – and it felt good.
- Visit all the NYC zoos. And the Aquarium.
- Log my books. I won’t resolve to read more – see above – but I am recording my reading, whether a whole book or part of a chapter, in my “Book Book” – a black and white cover bound composition book.
- Reread my advice to myself. I think kids asked for advice for a yearbook quote. And this is what I came up with, here: “Speak the truth. Work for Change. It’s not about you.” And expanded here: “Act against racism. Act against anti-immigrant bigotry/hatred. Act against sexism. Act against homophobia. Act for fairness. Act in solidarity. Looking away = acquiescence (and is absolutely unacceptable)” Figure this will drive what I do/say about Gaza, and about preserving medicare.
- Keep flowers in my apartment. I may grow some. I may buy some. I may buy plants that flower periodically. But this is easy, and flowers make me happy.
- Track my vitals. Won’t promise to lose weight or get more fit. But I resolve to pay attention.
- Ride as many of the NYC ferry lines as I can. Even Rockaway.
- Do not download games to my phone. I deleted all of them, one at a time, last summer and fall. I miss them – but like withdrawal – not like nostalgia. My screen time dropped immediately. Stay the course. Solid resolution.
- Have a good birthday! I needed one resolution that felt like a resolution. And three score is a lot. I should have a day or two to smile about it!
Interview with PEP member Tom Sheppard, Part II
Arthur and I discuss congestion pricing, and drug prices. I actually think what I wrote about congestion pricing was clearer. The point I make here, inelegantly, is that of all the things to go after Mulgrew for, this is not one of them. And the drug price stuff is a big deal – Arthur thinks we covered it – but it is a huge topic (involving large costs, and mega-profits).
The highlight is part II of the interview with Tom Sheppard, Bronx parent and PEP member. Starts about halfway through. Tom takes down mayoral control, school closures, and disparate impacts on communities of color. He also tells us about his big upcoming project.
Here’s Part I of the interview with Tom, if you missed it.
Feeling Congested? Pricing’s Not the Answer (repost)
[Note: Congestion Pricing is back in the news. Implementation may now just be a few months away. And Mulgrew just joined with some politicians to sue to stop it. Now, Mulgrew’s reasons may not make sense. And Mulgrew acted on his own, clearly did not even pretend to go to the Exec Board or the DA. But Congestion Pricing is bad policy, there’s much better ways to limit traffic, and it’s regressive, terrible tax policy. If it is stopped, that’ll be good. Read on. This is a repost from summer of 2021. – jd]
If all the major politicians in New York agree on something, it’s either a very good idea or a very bad one. Congestion Pricing is a very bad idea.
It has been played up in The New York Times. Cuomo has signed on. De Blasio is a proponent. Adams wants to hurry it up. All the defeated democratic candidates for Mayor supported it. There is pretty broad consensus among politicians.
New Jersey has an issue. And Sliwa doesn’t like it. Melinda Katz once opposed it – but I’m not sure if she still does. Residents of NYC had a pretty negative view until recently, but I think it’s closer to 50/50.
The idea is to charge drivers for entering Manhattan below 60th Street, with the amount of the charge varying depending on how crowded the Zone is. Result – fewer cars, less pollution, and a shitload of money to be used, at least in part, on mass transit. Let’s take the two big ideas – Reduce Congestion and Raise Revenue separately.
Reduce Congestion
I once worked, perhaps a few of you know, in transportation planning. I got curious when I saw Sam Schwartz speak at Brooklyn Polytech. Average Vehicle Speeds on Manhattan Avenues and Streets. I was immediately hooked. And while my actual work eventually involved mostly private bus lines that no longer exist, I never lost my fascination with traffic. I’ve read a bit more than a normal person should. Actually, more than a bit more than that.
Short version: You can cut down the number of cars entering the Zone. But you cannot cut down how bad the traffic is.
Longer version: People tolerate only so much delay. Make the delay worse, and some people will stop taking their vehicle in, until the delay is restored at the level the community tolerates. Reduce the delay, and more cars will flow in until the delay reaches the level the community tolerates.
Example for those of you annoyed by how counterintuitive this is: Recall when a road was straightened, or had a lane added. Recall how traffic moved better for a bit. And recall how other traffic found your spot, and filled it up. And how the delays returned to what they had always been.
Another example: Lane saturation was studied in England, and was the subject of an intelligence report from The Economist, drawing the same conclusion – add lanes? traffic will find them and congest them to the level that congestion existed before. Here’s a brief paper from Canada about this “rebound effect”.
Corollary: Remove lanes, and traffic will drop until congestion reaches the previous level. Great study from the EU – click here to look it over (other links here are brief – but this one is 50 pages)
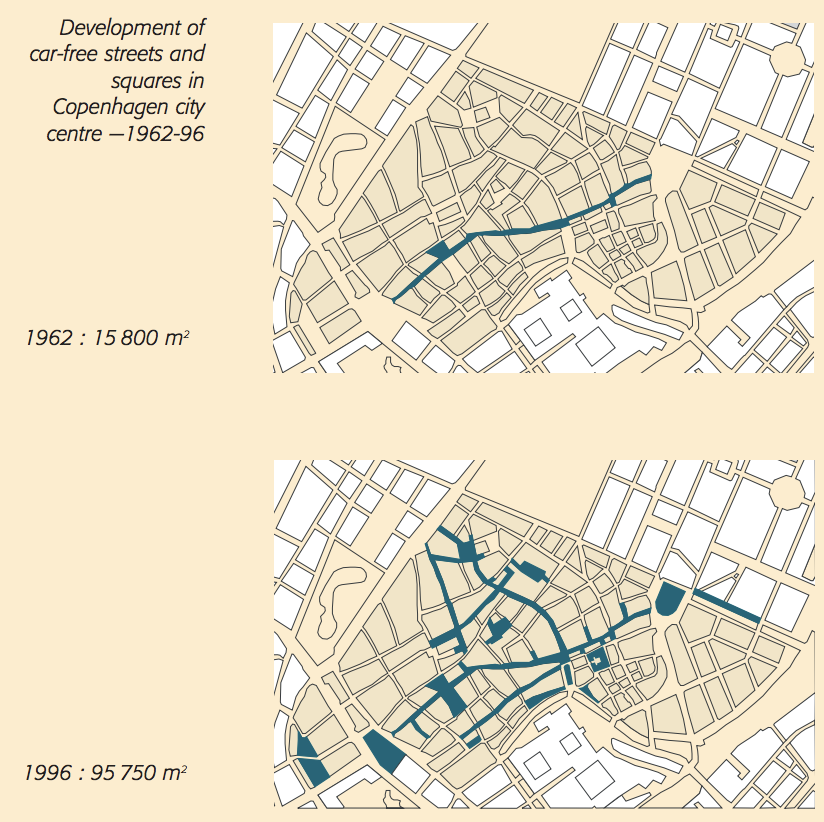
Conclusion: To reduce Manhattan traffic, remove lanes. Make more streets pedestrian only. Add consistent bike lanes. Add restaurant/commercial space (created from street space). The cars will still be delayed, but there will be many fewer of them.
Who will be affected? Well, everyone in the Zone will face less direct pollution from cars. Quality of life will be up. More walking. More outside seating, dining, etc, etc. Drivers? Those who most need access to Manhattan will deal with the worse delays. But those whose need is more marginal will opt for public transit, or not to take the trip. If the trip takes a long time, drivers will decide if it is worth their time.
Wrong conclusion: Congestion Pricing. Fewer cars will enter the Zone, it is true. But instead of those who really need access coming in, we will see those who can afford it. In fact, we will see an overall drop, but as part of that, wealthy drivers will replace middle class and working class drivers. Very Bloombergian. Zone residents might see nicer looking cars, but that is not a reasonable public policy goal. Plus, Congestion Pricing requires hardware and monitoring devices. Congestion Pricing draws an arbitrary line in Manhattan, and places an arbitrary boundary between one part of the City and others.
And a simpler and more effective method is available to reduce the number of cars traveling in Midtown and Lower Manhattan. Just close some streets, and remove some lanes. Nice story here about traffic “evaporating” when a popular link was removed from the London street system.
Side note, since I mentioned lanes. American lanes are wide. Wider than most other places in the world. Do you know what that means? It makes it easier to stay in your lane. Sounds good, right? Wrong. When lanes are narrower, drivers are forced to focus more on their position. They go SLOWER. Fat American lanes produce FAST American traffic speeds. And that contributes to this country’s horrible vehicle accident record, including a bad pedestrian vs car fatality rate. One of the most significant road safety reforms we could enact would be to narrow lanes. Google this if you want to learn more, or click this link that popped up when I searched.
Increase Revenue
Revenue? That’s money the government takes from some of us, and uses. If we are lucky, that money gets used for something that benefits society, maybe benefits us personally.
Taxes. We are talking about taxes. And who they come out of, and who they go to, those are very important questions.
it makes sense that taxes from car use go to fixing roads that cars use. Or does it? Maybe taxes from car use should go to making alternate forms of transportation better or more viable. Or maybe, just maybe, our taxes get jumbled together and repurposed as society needs them.
That last one, taxes don’t get used based on how or where they were collected, is the right answer. Taxes on parents do not pay for schools. We do not tax disaster victims to pay for fire service. We do not tax anyone based on how much trash they generate.
And in fact, this discussion (well, my discussion) is not about what taxes get used for. It’s about how they are assessed. And here we have choices.
Wealth taxes and luxury taxes – good. They are coming right from those who can afford them most.
Income taxes, graduated, with higher rates for higher income, and with a bottom below which no tax is assessed – very good. Progressive taxes. Done right, those at the bottom do not pay, those in the middle pay little, and those at the top pay a lot.
Sales taxes – regressive. We all buy “things” and so get taxed pretty equally, even while some people make much more than others.
Use taxes – even more regressive. This Congestion Pricing business might fall into this category.
Sin taxes – also very regressive. The paternalistic idea that cigarette taxes are to benefit people’s health is bs. Those least able to pay are also the least likely to feel the sort of daily control over their lives that would allow them to quit. These are regressive taxes, and bad taxes. Perhaps because of pollution some NY Times readers would categorize Congestion Pricing as a sort of sin tax.
Lottery – jeez – just rob the people least likely to be able to afford, thank you Andrew Cuomo. And some of those payoffs should be illegal.
Conclusion
Want to reduce the number of cars? Take away roads, take away lanes.
Want to increase revenue? Raise wealth taxes, luxury taxes, and marginal income tax rates on top earners.
Want to avoid bad policy? Stop this Congestion Pricing nonsense before it starts. Opt for solutions that work, and for fairness, instead.
2023 – Looking Back
January 3, 2023 I officially retired. So it kind of makes sense to look back from January 3, 2024.
So lets’ go for some highlights:
Highlights
January 3. I officially retired. I was on a cruise. We docked in Jamaica, and mostly I stayed in the touristy port area and ate a bunch of chicken patties.
Late January. Back to school! I started graduate courses in mathematics at Queens College. Apparently they thought I was a masters student when I did coursework there in 2013-14 (my sabbatical), so a little paperwork got me reinstated, and presto, I was studying point-set topology.
February was my birthday! I organized a walk in Van Cortlandt Park. Do you remember how mild last winter was? Sure you do. Do you remember though, one, completely out of nowhere, frigid day? That was my birthday. A crowd of 20 dwindled to five hearty souls. We walked 3 1/2 miles, visited the Van Cortlandt Mansion, and then got Vietnamese food. Everyone left, and I walked over to my barber. And he cut my hair and shaved me for my birthday!
May 12. I gathered some folks to mark my retirement. Nothing fancy, but felt nice to be surrounded by friends, colleagues, alumni, retirees…
Late June. I traveled upstate for a Juneteenth trip. National Abolition Hall of Fame (outside Syracuse). John Brown’s Farmstead (Essex County, near Lake Champlain), George Thomas’ grave (not really abolition, but adjacent), and the WEB DuBois historic site in Great Barrington, Massachusetts.
In July I got work! Math day camp for middle schoolers. Five weeks. Exhausting. But fun. We did the Pirate Problem and Ghost the Bunny and lots more math.
August was quiet… I went to Chicago for a weekend… spent other days hiking… And finished the month by starting two more graduate mathematics classes. It was also in August that I started preparing for the Retiree Advocate electoral campaign – we will be challenging Unity in the spring 2024 Retired Teachers Chapter elections.
In September I went back to Maine, to the same pond where I went the previous September so I wouldn’t be in New York when school started. Very peaceful.
In September I also started doing two math enrichment classes on Saturdays. Not test prep or homework help – just purely off-curriculum math with kids who, I don’t know, like math? Are curious? It was good. I’m doing it again in the Spring
October. In October it felt like the world turned upside down. I used to go to protests and demonstrations when I was younger, but not so much lately… until October. I think I’ve been in the streets more in the last three months than in the previous – I don’t know how many years.
October I also started a youtube thing with Arthur: State of the Union. We are up to once a month.
Honestly, the movement for a ceasefire seems to have overwhelmed the rest of the year. November and December were Thanksgiving and Christmas and calling for, if not peace on earth, at least an immediate ceasefire in Gaza.
Fighting Tuition Increases at CUNY, back in the day
I only got to New York City in 1984, so I don’t know all the history. But tuition increases were threatened in 1989, and there were a wave of protests and campus takeovers, and the increases were stopped. Here’s Ken Stein, speaking, probably to a group (bullhorn) from the roof of Schuster Hall (that’s Davis Hall in the background) at Lehman College.
In 1991 I was busy making calls, trying to coordinate work among campus coalitions across the city/area, against Desert Shield, which would soon become Desert Storm. Ken was the contact name at Lehman. And then after the invasion, there was another round of tuition increases, and another round of campus protests, less successful. By then I’d moved back to the Bronx. That’s when I first met Ken.
Time rolled forward. I went to Lehman. I became a teacher. I got involved in the union, a little, started going to Delegate Assemblies. David Shulman would often take me to dinner after the DA was over, sometimes with Cathy, or Cathy and Annette, and occasionally with bigger groups. One day we left Fashion Industries and went to a nearby restaurant. Big circle table, in the front, by the windows. I bet it was December or January, it was cold. And one guy looked familiar; Ken had become a teacher as well. He was at a place called Pacific. It got closed a few years later.
He friended me, or I friended him. Whichever. I started to see his photography – really amazing stuff. Some attractive. Some pure New York City gritty.
I’m not wading through to find more great samples of his work. It’s an impressive body. Please, when you have some time, figure at least half an hour, probably more, go to his Flickr, and take a look at some first rate New York City work. Or here’s an article about him (with older photos). And I think there’s more. I think his photos ended up in lots of publications.
In any case, I followed his Facebook posts, and looked at his photos, and read about cameras and lenses. We were aware of each other, but didn’t really interact. Until after he’d been at Forsyth for a while, and went looking to recruit teachers, and contacted me. I never was able to help, but I tried. And then he reached out for help with PBATs – again, I wanted to help, but it didn’t work out.
But that kind of set the stage for occasional interaction. He was real Bronx, and I was not. But I am here now – and so there were some mutual connections. His picture of himself at CBGBs, I showed it to a former student, now a teacher herself “Oh my god! that’s my pops!” (It’s Eddie Torres, the drummer. There’s also a Bronx Eddie Torres, a dancer. That’s someone else. I taught his daughter, too.)
Between 181 (did he live in Coop City? I don’t know.) and Lehman (But what high school? I don’t know) he had connections here. He once asked about his friend Andrea, who I do not know, but I knew the last name; I taught her daughter. He knew activists who I know, and Lehman folks, some of whom overlapped with both of us.
And we were both in the DoE, with some similar inclinations. We supported some of the same causes. You know when two people have photos from similar protests? He once asked me to donate to Samelys Lopez, that was back in 2020 – I was already working on a fund-raiser and recruiting volunteers. I developed greater interest in Consortium schools – Ken brought expertise. He asked about union elections – I gave him the run down – and I think he gave us his support. Lately we both have been posting for a Ceasefire Now!
I went to Ken’s retirement in 2021, a year before mine… Because he invited me. Cool people, glad to have been there. That was the third time we met.
And, sadly, the last. We were not close. Not friends. But the news hit hard. We were contemporaries. Some overlap in interests, at least political ones. And in New York. Similar background. Similar age. My heartfelt condolences to those who were close to him.
You can’t meet Ken now, but you can still see him through his work.
UFT Retired Teachers Chapter Election – coming this Spring
This spring, every chapter in the United Federation of Teachers will hold elections. In each school, a chapter leader will be elected to a three year term. In some schools para reps will be elected. And in each school, one or more delegates will be elected, depending on how many members are in the school. My high school, the HS of American Studies at Lehman College, we got one delegate. At Brooklyn Tech, which is huge, they got four delegates.
The “functional chapters” also hold chapter leader and delegate elections this spring – paras, secretaries, everyone. And the biggest of the “functional” chapters is the Retired Teachers Chapter (RTC).
Retirees elect not just a chapter leader, but a chapter leader, nine additional officers, and a fifteen person Retired Teachers Chapter Executive Board (not the UFT Exec Board). That’s 25 people. They also elect 300 delegates.
These elections are “winner take all.” And in every RTC election before this year, the winner was Unity Caucus. In fact, until recently, the elections were not even close. Unity would 80% – 90% of the vote, usually towards the upper end of that range – and they would consequently win the Chapter Leader, all nine other officers, the fifteen seats on the RTC Executive Board, and 300 delegates. Those delegates are delegates to the UFT Delegate Assembly.
At 90% to 10% the election results were not in doubt. For the opposition, Retiree Advocate (RA/UFT), they were a chance to share ideas with other retirees, even to let some know that an opposition existed. RA/UFT ran for Chapter Leader, the officers, RTC exec board, and maybe 100 or so additional delegates – didn’t matter because the result was not in doubt.
Medicare Advantage
Mulgrew and Unity changed that. In the spring of 2021 word leaked – the City and UFT and MLC had been secretly negotiating to remove retirees from Medicare and put them into a private Medicare Advantage program. Retirees were pissed, times three.
First, why change? We (well, those already on Medicare, which isn’t me, but I’m going to keep writing “we”) like our doctors. We are familiar with the system. We like public Goods, including programs from the New Deal and Great Society. We don’t like privatization. And we certainly didn’t ask for private care instead of Medicare.
Next, the negotiations were secret. Word leaked from another union. I can hear Unity already objecting “we don’t negotiate in public!” OK, but even if we accept that (and I don’t know that we should) – members expect to know WHEN they are negotiating, and over what. When there’s a contract, we know that the UFT leadership is talking to the City, and we have a rough outline of what they are bargaining over. But the retirees? Mulgrew kept them 100% in the dark. They were blind-sided.
Finally, the UFT leadership’s response, was, well… Mulgrew. Mulgrew tried to speak to retirees directly. He was speaking to zoom rooms full of pretty smart people. He spoke down to them. He pitched hard, and retirees knew they were being snowed. “Silver Sneakers” he told 100s, maybe 1000s of people who knew exactly what a “free toaster” is worth. Coming off like a used-car salesman would be bad enough, but he came off like a salesman, trying to sell to mechanics.
Competitive Elections
And what happened right away? RA/UFT’s vote doubled. Immediately. 30%. Highest ever. That’s not because RA/UFT was brilliant. It was because Mulgrew and Medicare. In the unionwide election the following year, 2022, the united opposition (including RA/UFT) again polled 30%. I did some analysis, here.
Now, 30% is not 50%. But that’s a big breakthrough. And if anything, over time, more retirees have seen Unity beaten in the courts, and looking awkward defending what can’t be defended.
I don’t want to bet. Going from 30% to 50% is still going to be tough. And, as Unity is in control of all levers of power, and is not afraid to cross lines and break rules, it’ll be even tougher. I’d call us (the opposition) heavy underdogs. But this is not 2018. We have a real shot, even if the odds do not seem to be in our favor.
Stakes
Chapter Leader of the biggest chapter in the UFT is a Big Deal. The symbolism of holding that office – it would be hard to underestimate the power of that. But there’s not much actual power in the chapter leader, and Unity would try to hamstring the entire leadership team, if the opposition won. But there still is some power. We could open up meetings to allow more representative member voice. We could serious discussion of serious issues back on the agenda. And we could officially register the RTCs strenuous objections to the Medicare Advantage scheme. That would make it tougher for Unity, if they were seen imposing this on retirees, against their will.
Bigger Stakes
In chapter elections in our schools, often the delegate (to the Delegate Assembly) is an afterthought (it shouldn’t be, but it often is). But retirees do not elect 1 or 2, or 4 delegates to the DA; we elect 300.
The Delegate Assembly often seems to be a loud theater, lots of noise, but in practice a rubber stamp for Unity. In the last few years however, that’s seemed a bit shaky. In the spring of the hybrid year (2020-21) Unity lost an endorsement vote – probably not because of the candidates, but because delegates thought Mulgrew was being a jerk. And then the following fall, Mulgrew mishandled the room and lost an important vote, and then completely lost it (his composure, the vote was already against him).
How do the RTC delegates fit into that? Well, there are 300 RTC delegates. Unity expects them to vote in “lock-step” (LeRoy Barr used the phrase speaking to me, explaining why they would not support non-Unity delegates to the AFT convention. While that is a different kind of delegate, “lock-step” represents Unity’s thinking in both settings). Anyhow, not all RTC delegates dial in, and not all of them vote as they are supposed to. But most of those who dial in, do vote how Unity tells them. I don’t know, maybe 150 are on the call for the meeting (just guessing) and 140 vote the right way? Those are wild guesses, but if correct, that’s a margin of 130 votes in favor of what Mulgrew/Unity wants on every motion and resolution.
Over the last year, vote totals for Delegate Assembly votes have been between 650 and 1050 (total votes, including both sides of the question). Most votes have had between 750 and 900 delegates voting. A built in +130? That’s really a lot, especially as Unity’s grip over the DA has at times seemed to be less firm.
But if RA/UFT wins? Let me pause here. In the last RTC election Retiree Advocate ran maybe 120 delegates. That was fine, when we knew there was no chance. But now there is a chance. Can you imagine us winning the election, filling 120 delegate slots, and the rest going to Unity by default? Not going to happen. We will absolutely not let that occur. We will run the full 300. Unity will as well… but they may struggle a bit. When they recruit AFT delegates, that’s easier for them, there’s a free trip involved. But that’s a different election. Delegate Assemblies – there’s no hotel room, no flight, no interesting city at the other end – you sign on from your couch. Since most Unity delegates are motivated by factors other than personal conviction, Unity may struggle a bit with motivation.
Let’s get back. If RA/UFT wins, a couple of things. Our Delegate Assembly attendance will be higher than Unity’s. RA delegates will be free to vote their conscience – we would expect nothing less. But on what for Unity may be key votes, that built in 130? Gone. They will have to convince delegates. And on stuff where Unity is dead wrong, like health care? Now think about 250 votes against them. And remember, there are only 900 or so votes being cast. Our 300 DA Delegates, should we manage to win, would be a game changer. The DA would no longer be Unity and Mulgrew’s rubber stamp.
A simple way to understand the UFT Healthcare Conflict
True Story
In the Spring of 2021 a story leaked
- – New York City and its municipal unions, including the United Federation of Teachers (UFT) had reached an agreement to switch retirees from regular Medicare to Medicare Advantage.
- Retirees in the UFT reacted. Many of them indicated they would “opt-out” – an option that looked like it would be available at that time.
- Mulgrew and Unity responded that this Medicare Advantage program was different from others; that retiree health benefits would be just as good, even better.
- The retiree vote against Mulgrew doubled in the Spring 2021 Retired Teachers Chapter elections.
- An organization for retirees from all the municipal unions formed (NYC Organization of Public Service Retirees), and worked through the courts to stop the plan. Many UFT retirees donated (and continue to donate to the NYC Organization.
- There was also an imposition of copays on retirees, which the City and the MLC (including UFT) supported. The NYC Organization was able to stop that in court.
- Today all is on hold. Retirees are still in traditional Medicare. The City (with MLC support?) is still appealing. Retirees keep what they have, at least as long as this standoff continues.
So, is this crazy retirees who hate the UFT and are trying to impede progress? And the UFT leadership (Mulgrew, Murphy, Unity Caucus) are just out to protect retirees?
Or are retirees fighting like hell to protect their health care, because it’s literally their well-being that’s at stake? And Unity/Mulgrew are, in contrast, interested in protecting patronage jobs and in honoring semi-secret agreements with the NYC Office of Labor Relations?
See – we don’t have to go into details about prior authorizations, co-pays, networks, the Stabilization Fund, etc, etc. There’s the Administrative Code, backroom negotiations, contract appendices. You can read about all of them. But you don’t have to to figure out the big picture. The picture is pretty clear.
That story was about retirees
Now Mulgrew and Unity are getting ready to make changes to in-service health care. That’s the health care for current teachers and paras and secretaries and counselors and other school personnel. Mulgrew and Unity are getting ready to change health care for all of you.
Think about what they tried to do to retiree health care. What do you think they are trying to do to you?
Are you going to thank them?
Or are you going to organize to stop them?
Help me create a puzzle
I don’t have a good puzzle for you today, and it’s about time for a little math, so I’m making one up. Or working on it. Weird thing about puzzles – you can make up a puzzle that someone has already solved. I think that’s what we’re doing, but let’s try all the same.
Since this is from scratch, we need to develop the topic before the question.
Topic: How many ways can we express a particular number as a product?
How many ways can a number be written as a product? So, what does that mean? First of all, by number we mean “natural number.” Then, what’s a product? For 10, it can be written as 
Do we have material for a puzzle? Well, let’s list out the first few.
| Number | Ways it can be written as a product | Show us |
| 2 | 1 |  |
| 3 | 1 |  |
| 4 | 2 |   |
| 5 | 1 |  |
| 6 | 2 |   |
| 7 | 1 |  |
| 8 | 3 |    |
| 9 | 2 |   |
| 10 | 2 |  |
| 11 | 1 |  |
| 12 | 4 |    |
So what kind of questions might we ask?
We could ask to have the list extended. Make it up to 20. Or up to 50. Or even 100. And we could ask for observations about what we encounter.
We could ask for the number of ways some larger number could be expressed as a product. Might be fun to try to count for, say, 350.
We could ask for the number of ways some much much larger number could be expressed as a product. If we chose, for example, 792,000, that’s big enough that you might not be able to count by hand, and would have to do some generalizing.
We could ask for some observations. Which numbers can only be written one way? (and why should that make sense?) Is there a relationship between the number of factors and the number of ways? The number of distinct factors?
We could ask for a formula to figure out the number of ways for a number in general. But, as I sit here, I don’t know the answer. And, as I sit here, I expect that the answer might be “complicated” in a way that goes beyond what most kids and much of my audience can handle.
We could ask for formulas to deal with some specific cases…or at least the descriptions of a solution. As a teacher I might have asked for a formula (or description of solution) for powers of 2, or powers of a prime, p. My students frequently confounded me by starting by looking at powers of 10 – but maybe that’s better for grasping some of the complexity here. It might also be helpful to ask for solutions for the product of 2 distinct primes (such as 
But I’m leaning in a different direction. 2 is the first number with 1 way of being written as a product. 4 is the first number with 2 ways. 8 is the first number with 3 ways. See that pattern? Think it breaks down? 12 is the first number that can be written as a product in 4 ways. What is the first that can be written as a product exactly 5 ways? 6 ways? Do you want to jump ahead? 10 ways? 20 ways?
Some questions
- How many ways can each number from 13 to 25 be written as a product?
- How many ways can 350 be written as a product?
- How many ways can 792,000 be written as a product?
- Which numbers can be written as a product in exactly two ways? Can you show that all numbers with this property can be written as a product in exactly two ways? And that no other numbers can be written as a product in exactly two ways?
- Is there a general formula here? (Let’s leave this out, unless you actually know the answer. I have a guess “yes” but I’m not certain what that guess would be, and I’m aware that it might involve math that I have not studied very deeply.)
- If a number is a product of n distinct primes, how many ways will there be to write it as a product?
- Consider the first number that can be written 1 way, the first that can be written 2 ways, etc, ie 2, 4, 8, 12, 16,…. what are the next five numbers on this list?
- Do you have a question I haven’t thought of?
I’ll try answering these (those I can) during the course of the week.
What do you think?
Is there fun stuff for kids to play with here? For us to play with? Would this make a reasonable activity? (and if so, how?)
And has all the math here been done before? (I’d be shocked if it hadn’t been)
I’m curious what you make of this.
Happy break!
On not being a rubber stamp – Tom Sheppard, Episode 3 of State of the Union
This episode Arthur and I interview a Bronx ELA teacher, Rebecca Torres, and Bronx Panel for Educational Policy member Tom Sheppard.
Tom has been outspoken on PEP – and he doesn’t disappoint on the podcast – he discusses how he got involved, equity in terms of facilities, and then he starts on the PEP and governance and mayoral control…
By the way, there is a part II of Tom’s interview that will be in the next segment.
I’m really enjoying the teacher segments – love the fact that Rebecca had a strongly held idea, and modified it – because that made sense for her students. Were the people in charge half that reflective…
Comments, praise, criticism, praise, all are, as always, welcome and appreciated.
Здравствуйте, Ёжик!
Mystery, right?
In computer programming, when you are trying to get a new language to work, and want to check syntax, you try to get a program, usually just a line or two, that prints on command. If you are successful, you are greeted with “Hello World.” Serious. Go on. Google “Hello World.” See. I wasn’t making that up.
Hello, World!
In DuoLingo you learn lots of weird words, and useless phrases… For a few years I binge watched a bunch of “Nordic Noir” movies and series. The genre originally came from Sweden. Slow-moving. Sometimes plodding. Police procedural dramas. Hero has been traumatized, or is somehow psychologically off-kilter. Or just sad. Shows popped up across Scandinavia, and in Britain and Northern Ireland. There was a weak remake of one done in the US. Broadchurch was award-winning, or should have been. I’m too lazy to look it up. Shetland was alright. I loved Happy Valley – although for these depressing creations I’m not sure “love” fits. The Fall in Northern Ireland, with Dana Scully playing an actor playing a detective. A bunch in Finland, Norway, Iceland, etc. By my absolute favorite was Hinterland. It was set in Wales. One episode I was watching (this was all in English by the way) and a local doesn’t like our detective, and says something. From the tone of voice, it was mean. But the words? They were not English. I was curious, and started digging. Apparently I was watching one version. The other version, the hit version “over there” was filmed bilingual. It was complicated. Some characters were Welsh-dominant. Some code-shifted effortlessly. And some were less comfortable in Welsh. And there may have been some English characters who didn’t know a word (and no, that does not include the detective. He lived in England for a long time, but was in fact Welsh, so while his Welsh was uneven, he did speak, and he gets better through the show). And to make this happen, the actual cast was all bilingual, and each episode was filmed twice. Ok, so now I see a few episodes in the hit bilingual original. Called Hinterland in English, and Y Gwyll in Welsh. Too cool. I go to DuoLingo and say “teach me Welsh” and I spent a few weeks, and all I remember is “Bore da, Draig!”
Good morning, Dragon!
Which brings me to the title of this post. I am using WordPress. And not writing frequently, or at least not consistently. And if I ever had a fanbase, I’ve lost most of it. But someone named Eozhik is liking most of my posts. Funny looking name, right? Except I think I recognize it. Eo sound like “Yo!” and if it were in Cyrillic would be written as an e with two dots: Ё. Zh sounds like how a French speaker would say “jour” as in “Bonjour” – like a sh with the voicebox vibrating. There’s a Cyrillic letter for that, too: ж. And ik? Like Ick. In Cyrillic just an “ee”+”k” = ик. And put them together – we get Ёжик, which is apparently the name of my new fan. It’s also the Russian word for hedgehog.
Greetings, Hedgehog!
UFT High School Vice Presidents – with some narrative
George Altomare, who passed earlier this fall, was the first UFT HS Vice President. Of course I did not meet George until years after he had retired. He was on the UFT Executive Board – I think for the entire 11 years when I served. He used to promote the New York Association of Social Studies Teachers conferences. (New York Council of Social Studies Teachers? Not sure of the right name). He also used to play on his guitar to close out conferences – which songs did he play? Was it Solidarity Forever? Yup, he played at every AFT convention I went to. George lost the vice presidency to Michael Shulman in 1985.
Michael Shulman represented an opposition caucus – New Action. In 1985 he beat George Altomare head to head for HS VP, fair and square. But the union’s leadership grouping, called Unity, sued to overturn the election (that they had conducted!) A second election was held. Shulman won again. George retired the day the result was confirmed. Shulman is the only Vice President in the UFT’s history not to come from Unity Caucus. More on that below. Shulman served one term, and was narrowly defeated by John Soldini. Mike returned to the classroom, I believe at Fort Hamilton High School.
John Soldini (Unity), Shulman and Altomare were the only three HS VPs to be elected directly by the members in the high schools. Unity, desperate never again to lose the position, converted all the VPs to Vice Presidents at Large. Up to that point, high school teachers elected the high school vice president. After two amendments, all UFT members – teachers, paras, secretaries, retirees – from high school, from middle school, from elementary school, from everywhere else the UFT represents people – all of them voted for the “Vice President at Large for High Schools.”
Soldini was high school VP for over a decade. Sometimes he would have been the choice of high school teachers – but usually he lost among high school teachers, but remained in his position. The change in rules ensured that with solid backing of elementary teachers and retirees, John never again had to worry about high school teachers choosing someone else.
Soldini was VP when I came to my first high school level meetings. They were raucous affairs – high school chapter leaders challenged him on many items, and he pushed back hard. I definitely remember a few shouting matches. I also remember packed meetings, and sandwiches (I didn’t come for the sandwiches). There was real discussion about real issues directly facing schools. Of course that was before the massive break up of the high schools… What were there? 100 high schools in the city? And most of them sent their chapter leaders to listen to or yell at John.
When Soldini retired, Unity chose Frank Volpicella to be the next HS VP. An aside, my District Rep, David Shulman, thought he was in line for the post, and retired when he was not tapped for it. He didn’t speak about it, but I think he remained bitter.
Frank was stepping into a mess, with the break-up of the large high schools in full swing. Unity, which had signed onto the plan, was now backing away (though without much real opposition – dropping the responsibility on each individual school to put up its own individual fight, and we watched loss, after loss, after loss). In any case, there was a swarm of activity, but I don’t remember much about what Frank did. He was regarded as a nice guy – in fact once he said something really insulting about me – but I spoke to him, and he quickly and graciously retracted it – not everyone has that same sense of decency. In any case, now I was going to high school level meetings regularly. And among other things I noticed, attendance started to fall.
Frank retired in 2007. The high school division almost died when he left. Frank’s successor was a supporter of school reform. One time he explained that breaking up the big schools and their lazy chapters would inevitably give rise to a new cohort of active chapter leaders in the small high schools. It seemed unlikely then, and history has born out how completely full of shit he was. The fights against closing schools were hamstrung by having a VP who wasn’t really opposed. On big politics, his role at AFT conventions – introducing one pro-war resolution after another, was sickening. And there was not even something personable about him that mitigated the other stuff; I once sat with him, one-on-one, as he offered me a job (that I did not take) and during those ten minutes that seemed like an hour not once did he make eye contact. As an ideologue and a boring speaker who did not really listen to anyone else, the high school meetings became dreary. Attendance, already dwindling, plummeted. I recall once sitting in the room, in his High School VP’s meeting, and realizing that me, Zulma and Sam, 3 chapter leaders from the Bronx, all from small schools, were the only chapter leaders in the room. Everyone else were DRs and paid staff.
When Janella Hinds was appointed/elected (by the Exec Board), it was a breath of fresh air. Let me back up – the Exec Board election was actually an election – October 2012. I was nominated by New Action – and lost, 67 – 7 (never figured out where the 7th vote came from, there were only 6 New Action exec board members. I do know that Michael Mendel scolded me for asking for the count.) In any case, Janella was open to conversation, and committed to rebuilding the meetings in the HS Division. Lots of damage had been done, but slowly the meetings built back up. Now, with all the mini-schools, and the four hundred something high schools, attendance is not like in Soldini’s day… but in Janella’s first year or two there were times when we wondered if they would ever come back – and they did. Now there are high school events, high school awards, and some sense of a living division.
The electoral history since Janella’s election is interesting. She won in 2013 – both by Unity’s rules, and among the high schools – New Action and Unity combined to give her almost 60% of the votes against MORE. But in 2016, while she won (it’s a VP at Large), high schools actually preferred James Eterno roughly 51% – 46%. In 2019 she won both the total vote, and with high schools, over 68%. And in the latest election I won most of the high school votes (56%), but Janella prevailed in the other divisions, and since this is now an at-large – retained the position, 66% – 34%.
I wrote a High School Vice President electoral timeline earlier this fall.
Giving Season
I visited a friend this weekend – she had a present wrapped for me… I was embarrassed – I got us a nice lunch. I was caught flat-footed. I think of Christmas Season starting about 6 days before (like today, but I have final exams, so, for me, tomorrow). I know that’s old-fashioned. Christmas starts earlier and earlier. After Thanksgiving? After Halloween? The day before Labor Day?
But the personal presents aside, December does conjure up feelings of “giving season” to which I am not immune. With so many causes, how do you choose? I guess the decisions can be arbitrary. Here’s mine:
Rosenberg Fund for Children
I started donating three years ago. I was, more than anything else, recognizing the work of Abel Meeropol, who with his wife Anne adopted Ethel and Julius’ sons after the US government executed the parents. Abel had been a teacher - high school English, DeWitt Clinton, up the block from me – (Abel was never a UFT member). He was also a poet, and a songwriter – his most famous work was Strange Fruit. Anyway, donating to indirectly recognize Abel is a little convoluted – he DID help protect children of activists who were being abused by the system – but I think it’s perfectly okay – whatever the reason.
In the intervening years I learned a little more about RFC and its work. And just now I’ve been reading Robert Meeropol’s “An Execution in the Family” – and I was in the chapter on the founding of the Rosenberg Fund for Children when the appeal came in my mail and email. I think I understand better what the organization does, and feel even more motivated to help.
The Rosenberg Fund for Children was established to provide for the educational and emotional needs of children whose parents have suffered because of their progressive activities and who, therefore, are no longer able to provide fully for their children. The RFC also provides grants for the educational and emotional needs of targeted activist youth. Professionals and institutions will be awarded grants to provide services to beneficiaries.
– RFC website
I had been giving late January/early February, but the timing of the appeal worked – I gave. And I’ll donate again on my birthday. Here’s the link: Support the Rosenberg Fund for Children.
The International Dreamers Scholarship Fund
There are probably thousands of good causes to help high school students – I worked from the 1990s as a high school teacher – and this is one of them. It also caught my attention a few years ago, I got tagged on Facebook I think. The organizer is a daughter of a friend – the friend is Fred, daughter Jessica (who I feel like I know a bit, even though we’ve never met).
For over a decade this fund has been supporting students without documentation as they go to college. It supports vulnerable students. And it helps build community (not mine, but that doesn’t matter).
Dear Friends and Family, For the past 10 years, my school has supported a very special project: The International Dreamers Scholarship Fund, which helps undocumented graduates of the International High School at Prospect Heights (the school where I teach) go to college by helping to pay their college tuition. Since we began in the Spring of 2013, we have awarded over 30 scholarships. In January of 2019, the passage of the New York State DREAM Act made state financial aid available to undocumented students who arrived in the country before their 18th birthday. However, these students are still unable to access the federal loans and and grants that so many students need to cover the other costs of their education and are similarly blocked from employment opportunities that might enable them to cover some of those expenses out of pocket. As a result, the International Dreamers Scholarship is committed to continue supporting our most vulnerable students. Please donate below to help support this project that is very near and dear to my heart. Thank you.
– Jessica
And so I started giving a few years ago, and am happy to contribute each year.
Here’s a link to: Support the International Dreamers Scholarship Fund Facebook Page, and another directly to the International Dreamers Scholarship Fund donation page.
Ceasefire Now
Some giving is about a donation. But there is also giving your time, your energy, your voice. In the case of Gaza the need for an immediate and permanent ceasefire is clear.
And so I give my activism. Some are great organizers. There are many, but I am calling out one: I am amazed at the work that Jewish Voice for Peace has been doing. So important. So impressive. The slogan “Not in our Name” – the high visibility protests. The songs. I am not an organizer, but I can bring my support.
And so I give my voice. Others have bigger audiences, or speak with more clarity, or can share direct experience. But as each individual who opposes the bombing, the killing, the destruction, the hunger – as each one of us gives our voice – it makes it easier for others to join in. I’ve noticed that some don’t try to change my mind, they just ask me to remain silent. No. Remaining silent is not an option. I give my voice.
Children
I guess that’s my theme. This year. I think it’s a good one.
Honestly, in the past I was not moved by the season. Presents? Donations? Bah.
But now, older, in my very very early 60s (that’s what I call 59), it’s different.
So yeah. This is what I did and am doing. Makes me happy that I am making good choices.
COVID’s Lost Generation?
The New York Daily News just completed a three-part series, “COVID’s Lost Generation”, on the aftermath of the COVID pandemic – as it hit New York City school kids. (Behind a paywall, sorry, Part I: NYC school kids still face devastating fallout, Part II: Isolation, Anxiety present challenges to NYC school kids, and Part III: Money, time, running out for NYC school kids left behind.)
The stories are personal, and you feel for the kids. It’s well written. I happen to think that Bamberger is one of the better NYC ed journalists at this time. But the story is more complicated than compelling personal stories.
You probably can predict the narrative: Everything was good, even great. Then abrupt school closures. Disruption. Closures lasted too long. Students did not learn. Disconnected. Lost. When school finally came back, there was “learning loss.” Can’t catch up. Students were harmed emotionally. Some won’t come back to school, or are now chronically absent.
And while bits of that happened, let’s remember the big picture, the way it played out in New York City. Let’s look, or at least start to look, at the mistakes that teachers knew about, and the mistakes that leaders continue to make.
Timeline
Let’s remember some timeline – schools closed March 2020, and the closure was extended twice, until finally mid-April they announced schools would be closed until the end of June. During that time we were supposed to teach remotely. There was no actual guidance from the DoE on remote teaching. And there was precious little sharing of experience. Each school made it up as it went along, on its own. Mulgrew’s emails were infuriating “we got this” – well no, “you” are not “we” – and just no, why would you tell people who were struggling that they are doing fine? It was draining and stressful and just horrible to have the city turned upside down by the pandemic, and not to have support.
That spring and summer the DoE and UFT worked on the premise that some sort of “hybrid” schooling would be in place for at least the start of 2020-2021. Hybrid, I wrote about it at the time, was a very very bad idea. The idea that teachers would somehow teach remotely and live? Nah. It made no sense. I first learned about it when I was meeting with other UFT programmers, and one of Mulgrew’s reps showed up and told us to find a way – and then told us not to worry about details (we were programmers – so that was not going to work). Later I complained to DoE insiders I know – and I got the same reaction from all of them – “hybrid” did not come from the DoE – it was pitched, hard, by the UFT.
The planning over the summer got worse and worse. I am convinced that “Instructional Lunch” was also a UFT-inspired plan. The ventilation checks were comical. The space considerations had moving goalposts. And then the UFT made a big show of threatening strike action. Not over needing to go remote. Over testing.
And then schools opened, some. Not high schools. And there were delays. And opens and closes. And hybrid. It was weird. The whole year was like that. And then 2021-2022 we were back in person.
We lost a year and a half of schooling. We had some remote instruction. It went ok in some places (including my school), mixed in many places, and bad in a lot of schools. There WERE kids who never really signed on, who drifted away without the social interaction.
Remote Instruction
Little reality check. There was at no time a serious effort to improve remote instruction. Sure, some schools worked at it. Many individual teachers worked at it. But the UFT leadership offered little better than Mulgrew’s infuriating “we got this!” (Mission accomplished?) which wasn’t true. And the DoE always threw the responsibility onto principals, the majority of whom were poorly equipped to address remote instruction (and too many of whom are poorly equipped to address regular instruction).
Remote instruction sucked, but there was no attempt to improve it, to make it better. That seems to have been intentional. Carranza never initiated any joint work on studying or analyzing or improving remote instruction. And Mulgrew was so committed to telling the whole world that NYC schools were open (no matter what was happening on the ground) that he wasn’t going to risk that narrative by talking about remote – even though that’s exactly what teachers and kids needed.
So that’s a sore point, as I read the Daily News articles. Remote could have been better, if we’d try (and by we, I mean Carranza and Mulgrew), but we (RC and MM) apparently didn’t try, and didn’t want to consider trying.
My school, all instruction was remote, and we definitely got a better schedule than most schools, and we got better at teaching. It still sucked, but probably a lot less than at most other high schools. Hybrid would have been worse. Zoom in a room – that’s another post – was definitely worse.
Connecting
Hey, this was bad. There were kids who completely disconnected. There were kids who substantially disconnected.
And we’re back!
In some ways, the worst part of this narrative is the return.
Imagine you are in a movie theater. Technical issue. Movie stops playing. Twenty-five minutes. And then it starts again, not where it broke, but twenty-five minutes later. What do you do?
If you are me, you tell them to “rewind” or whatever they do today. Let’s pick up where we left off, right?
If you are the DoE, you keep playing, 25 minutes ahead. And then they moan when people walk out of the theater. This is a management problem, not an “attendance” problem.
That’s what the DoE did with schools. No attempt to adjust curriculum to meet students where they ended up, after a year of pandemic, of disconnection, of remote learning (not optimized, because Carranza and Mulgrew didn’t want to be seen as supporting remote learning). No, the DoE pushed schools to keep their regular curriculum, to get back to normal, and not to attempt to meet the needs of our students.
Of course they did suggest social and emotional learning – but as a non-tested suggestion – you can guess what happened in many schools, maybe most schools. Those who already attuned to their students’ emotional needs paid more attention. And those schools that were not, did not.
And then there is “Learning Loss.” Or actually, no there’s not. There’s no such thing. Learning Loss is a misleading label, a claim that kids know less now than before March 2020. Bunk. Kids learned less than they might have – but actually lose learning? Nope. When opponents of public education talk about learning loss, what they point to is that test scores of kids who came through the pandemic are lower than similar kids previously. Kids during the pandemic learned less than previous kids had during regular years. That’s not “lost learning” – it’s just “less learning” and was totally expected.
And this talk about “catching up” – they don’t mean catching up. They mean starting the movie 25 minutes ahead, and watching kids struggle. That’s not catching up. That’s bad pedagogy. That’s actually being mean to kids.
Summary
The pandemic was horrible. The effects on schools were horrible. But the DoE, and the UFT leadership, made it much worse than it had to be.
- They wanted to announce loudly that NYC schools were open, and so they refused to help improve remote instruction.
- Their decentralized approach guaranteed no Social Emotional support in the places that already had the least.
- There was no attempt to adjust curriculum to match what students now knew.
- Instead there was a demand to “catch up” – totally unreasonable, and kind of mean.
- The language of “learning loss” does not reflect reality – no one “lost” learning, (and consists largely of comparing kids to older kids who went to school without COVID)
And finally, I’ve been kind to the NYDN, but “a lost generation”? This is a tough story, what happened was not good. But a “generation?”
I’m Sticking with the Union
I got a slick-looking promo in the mail this week – a 6″ x 9″ folded, colorful piece – offering to save $850 a year – if I quit my union.
Hell, no!
Post-Janus, teachers no longer have to belong to their union, or to pay an agency fee. But most, the overwhelming majority, have stayed. But there is a lurking threat. And there are right-wing, anti-worker groups that have their sights set on destroying us.
The Freedom Foundation is who sent me the promo. The postcard (that I am not filling out!) looks like it is addressed to NYSUT, but actually goes to these rightwing frauds, authorizing them to disenroll you from your union. Don’t be fooled.
Our union, imperfect as it may be, is a vital part of our working selves. Any rights we have – were won through the union. And without the union the employer (the DoE) would be unconstrained from taking those rights back. When the union does not seem to fight hard enough, that’s a reason we should work to get it to fight harder. But make no mistake – our work would be far, far worse without our union. I’m sticking with the union. You should, too.
Right after Janus the Freedom Foundation and similar scum tried to undermine our unions. At least in NYC, with the UFT, they completely failed. Teachers knew not to quit. And new teachers still signed their union cards.
They will probably fail just as badly this time. Teachers should not be fooled by the dollar sign – this is anti-union crap.
But it is a hard fight. And it does not help that the union leadership has done some pretty lousy stuff. Exhibit A has to be the fight over medicare. Why would Michael Mulgrew want to force retirees, against their will, into Medicare Advantage? Why institute copays? Why remove popular Borough Rep Amy Arundell, and refuse to discuss the move? (sign here) And there’s more. It certainly feeds into a sense of cynicism – which could lead some teachers to misguidedly fall for the Freedom Foundation’s garbage. When Unity makes bad moves, it makes it harder with those of us, deeply loyal to the union, as we fight on behalf of the union.
Adding Fractions Wrong
Everyone knows… (that’s a bad way to start a post)
To add fractions:
- if they have common (same) denominators (bottoms), we add the numerators (tops) and keep the denominators:
and in general
- If they do not have common denominators (bottoms are different), we change the fractions to equivalent fractions (same value, different look, like and ) with common denominators, keep those denominators:
Or, instead of making two separate cases, multiply each numerator by the other denominator, and take the sum (that’s the numerator) and multiply the denominators: 
Adding wrong
I see kids add fractions wrong. Hell, in the US we can see adults add fractions wrong. Numerator plus numerator, denominator plus denominator. Tops with tops, bottoms with bottoms. If you haven’t seen it, you’re not looking.
If we want to add 1/2 a pizza and 1/8 of a pizza (a slice) we don’t get 2/10 of a pizza (less than half). The idea that this is adding is ridiculous.
But tops + tops over bottoms + bottoms DOES produce a result. Let’s name this process – I’ll call it MISADDING – and see what MISADDING actually does.
MISADDING
Being formal, define MISADDING as
A few days ago, Dave Marain published this:
It reminded me of MISADDING. On Saturday I played around with MISADDING with some kids, and talked about it a little bit with a mathematician. Here is some of what we decided:
- MISADDING
is commutative, since the underlying operation is regular addition.
- MISADDING
- Take a fraction, and MISADD
or
and in general
.
- MISADDING
and.
Those answers are equivalent.
But MISADDING? Uhn-uh.
but,
hardly the same thing. - MISADDING
then
. There’s a pretty straightforward proof, if you’d like to try it.
- MISADDING
. Nice, right?
- MISADDING
than if you MISADD with
.
- If we drop the notation, and write the fractions in parentheses with a comma, MISADDING
- MISADDITION
- Combining the vector idea with the in-betweenness idea, we could see the pairs (or the fractions) as an expression of slopes… Rewrite this
as (b,a) + (d,c) = (b+d,a+c), and now think of (b,a) as the line from (0,0) to (b,a) and its slope will be
. Vector addition will give us a point with an associated slopes between the two given slopes, UNLESS the points are on the same line, and then the result will be on the same line (equivalent to MISADDING two equivalent fractions, and getting an equivalent fraction as the result).
Too long, didn’t read version:
When you misadd fractions by adding the tops and adding the bottoms – the result will not be greater than the two originals (which is what you expect for adding positive numbers) but IN BETWEEN them.
And if you came here for a post about Mulgrew… (I’m stopping here)
How small an area?
I sometimes write about mathematics. This is not a post about mathematics. This is a post about Palestine. This is a post mostly written for New Yorkers.
I support an immediate ceasefire, and a permanent ceasefire. But this post is not about a ceasefire. It is about area. It is “geometry” in the sense of “geo” + “metry” or “Earth” + “measurement.” It makes distances and areas in Gaza more understandable by comparing them to distances and areas we (New Yorkers) are familiar with.
The Gaza Strip is small. Everyone knows that. But most people don’t have much of a sense of the size of things. I am writing to help you understand area and distance.
I read somewhere that Gaza is the size of Manhattan. I knew that was not true. Gaza is bigger. And I saw some detailed maps from the BBC. And they had scales of miles… and I knew I could make the numbers more meaningful for readers.
The Gaza Strip is 141 square miles. Brooklyn (70) + Queens (108) are 178 square miles combined. The Gaza Strip is about 80% the area of Brooklyn + Queens.
Those scales are pretty close –
Gaza is 25 miles long (roughly). The distance from Seagate (past Coney Island) to Fort Totten (past Bayside) is a 23 mile walk (according to Google Maps). As the crow flies it’s probably closer to 20. And so on the map, measure the length of the Gaza coastline, and measure the distance from Sea Gate to Fort Totten. Should be close, with Gaza about 25% longer.
So Gaza stretches a little longer than Brooklyn and Queens combined, but only 4/5ths the area. “Narrow.”
Israel limits (before the current conflict) Gaza’s fisherman to 5 miles from shore. The same limit on Brooklyn/Queens boats might get them to the tip of Sandy Hook, but not the Jersey Shore, maybe Great Kills, but definitely not Tottenville, parts of New Rochelle, but not Mamaroneck. (Blue for yes, or maybe. Red for no.)
Brooklyn and Queens have combined about 4.8 million residents. Gaza has 2.3 million. That makes Brooklyn and Queens denser – at about 27,000/square mile – than Gaza – at about 16,000/square mile. On the other hand, Gaza had far less housing (before October 7). Overcrowding was already a real problem.
When the Israeli army ordered Palestinian civilians in Gaza to move south, this was the territory north of Wadi Gaza, about 60 square miles, a little smaller than Brooklyn. That’s about 40% of the area of the Gaza strip. Likewise, Brooklyn is about 40% of Brooklyn and Queens combined. So it’s something like ordering everyone living in Brooklyn to move to Queens in a few days or become a “legitimate target.”
But unlike Queens, the Israeli army has destroyed or made uninhabitable half of all buildings in Gaza. (the red bits on the map below.)
The Israeli army has now ordered most Palestinians in the south of Gaza to evacuate. Where? There is a “Masawi Humanitarian Zone” in the southwest – less than 4 square miles. (see the BBC map, above). This is a bit smaller than Canarsie. 2.3 million people, even with the worst crowding, could not possibly fit.
I can imagine people who have never left Brooklyn or Queens, their whole lives. It definitely happens. But it’s a choice. And even for most of them, there was probably a trip into Nassau, or an occasional foray into Manhattan.
For Palestinians in Gaza? Most have lived where you see, in the maps, and have never left. Never traveled. Never seen “the River.” Not their choice. And as tiny as that world is, imagine losing 40% of it overnight. 50% of the buildings. And now, really, 95% of the space? I can make the numbers real, but it is not just numbers, and what it is, that reality I cannot begin to imagine.
Finding School Survey Results (NYC)
Want to know what teachers think about a school? Best way to find out is to talk to those teachers… but that’s often not an option. And especially for teachers considering transferring, it’s important to get some idea of the mood and relationships – stuff that never appears on the school’s website.
One option is to check what teachers wrote on the school surveys. Now, this is not a perfect option. Many teachers do not fill out the surveys. Many do not trust that they are anonymous, and fill them out to please their administrators (I DO think they are anonymous. I encourage people to fill them out honestly). But this means that the surveys MIGHT reflect more positively than they should. The surveys can give a falsely upbeat view of a school. But a negative result on a survey – that’s a pretty good indication that there may be a problem – certainly I would recommend doing further research before accepting a position at such a school.
A positive result on the surveys might be meaningful, might not. I don’t put much stock in them.
A negative result on the survey is usually a clear warning that there is, or was, a problem. That’s a warning alarm. Do check to see if administration just changed – but otherwise – uhuh. Probably that’s a no.
In the past I published some results from these surveys. That’s years ago. I have time; I should get back to that. Gene Mann publishes abbreviated results for Queens (I think), which is a service.
But let’s say you want to find the results on your own. I am going to look at two neighboring middle schools in District 11 in the Bronx, 180 and 181. How do you we find them?
I generally do not navigate directly to the page, since I do not trust Panorama links to stay stable. I start at: https://www.schools.nyc.gov/about-us/reports/school-quality/nyc-school-survey and click the 2023 Survey Data and Analysis link.
That link brings me to this page: https://infohub.nyced.org/reports/students-and-schools/school-quality/nyc-school-survey and then I click on 2023 results:
Which brings me to the first Panorama page https://secure.panoramaed.com/nycdoe/understand:
Everyone wants to click on the red/orange “3151 Schools” first. I don’t. I start by clicking the blue buildings on the upper left “NYC Public Schools” – and I see a weird table (which I don’t care about):
In the upper left there are some options. “City” is highlighted. Change that. Click “School”
and we move to a massive table, with lots of colors. Adjust your window to fit as much as you can:
Those colors – the deeper greens are for good results, the rustiest red/oranges are the worst. The schools are listed by district, so I’m going to scroll down a bunch to reach District 11, where 180 and 181 are. I put the two schools on one screen:
Wow, that’s a lot of data. What to look at first? I suggest the three columns in the next to last group on the right: Teacher Influence, Teacher-Principal Trust, Teacher-Teacher Trust.
At this point we have our first order answer – teachers at one of the schools trust their principal. At the other, nope.
There’s more we might notice. At the second school, the principal trust box is one of the greenest – in other words – place may not be perfect, but teachers like the administration. At the first school, with lots of poor and mediocre ratings (from kids and parents too) I notice that safety is better than the other ratings (both teachers and kids say so). Probably doesn’t make up for the overall ratings, but something to think about.
Sometimes looking at which numbers do not fit the picture raises interesting questions. Kids love the school, adults don’t? What’s going on there. “Instructional Leadership” is much lower than “Teacher-Principal Trust”? Might be a “nice guy, can’t run a school” situation. And the reverse, instructional leadership is well-rate, but teachers don’t trust the principal? Things to think about.
Let’s go back and take a look at the individual schools. Find your way back to the first Panorama screen, but this time pick the red/orange building that says 3151 schools:
When you click on the building, you get a search list. Scroll down to your school, or type in the name:
And then click it. You will see a big set of blue bars.
That is the student results. Look at the top of the screen, and flip to teacher results:
Now, we have lots of options to choose from. This is 180, I’m going straight to Teacher-Principal trust, because that was what concerned me most. (Don’t worry about the blue bars, just find your question)
Turns out, there are a bunch of questions that go into Teacher-Principal trust (near the bottom of the list). Unfortunately, they don’t point to an alternative narrative.
I do notice that the numbers have all fallen a bit from what were already sub-mediocre scores the year before… but I don’t see anything that makes me curious to dig further.
Limitations
I want to be clear – the surveys don’t get everything “right” – they are what staff filled in. Maybe the staff was angry that day. Or maybe they filled in the survey with the principal standing over them. Lots of things could mess up the data.
But when a staff fills in negative information, I think that is at least a signal that you should look more closely.
And when the ratings for a school are consistent (high, medium, mediocre, low) but one or two scores buck those trends, I pay A LOT of attention to those exceptions, and you should too.
State of the Union w/ Arthur and Jonathan Episode 2
This episode is devoted largely to two teachers, chapter leaders, activists, who used to work for the United Federation of Teachers, but who got fired for thinking the wrong thoughts. We also talk about class size and To Kill a Mockingbird. And there’s an interview with a really dynamic math teacher (not me).
By the way, watch that teacher segment closely – it was fun to do – and we would like to do more of those.
Comments, praise, criticism, praise, all are welcome and appreciated.
JD2718 