Logic puzzle. One answer? Or two?
October 1, 2007 am31 7:19 am
A friend asked me to post this. He claims there are two correct answers. I only count one. What do you think?
A professor entered a lecture hall and saw four students: Patricia, Quentin, Roger, and Sara. On the lectern was an apple. Curious, he asked each student who had brought it. Patricia said “I did not bring it.” Sara said “Quentin brought it.” Quentin said “Roger brought it.” Roger said “Quentin did not tell you the truth when he said I brought it.” Only one of those statements is true. So, who brought the apple?
And while you are playing with that, who is this problem appropriate for? In what context would you suggest using it?
JD2718 
Thinking out loud…
Q saying “R brought it” and R saying “Q is not telling the truth when he says I brought it” cannot both be true. They also cannot both be false, so one of them has to be the true statement.
If R’s statement is true, all the others must be false. This means P brought it. This works — P is false, Q is false, R is true, and S is false.
If R’s statement is false, Q’s must be true, in which case R brought the apple. But that leaves P statement true as well, so that solution doesn’t work.
So I only get one solution…
I’d think that middle or high school students with some experience with logic problems would get it… I’ll try it out on my daughter.
My only quibble with the above is trying to figure out how Rachel can have posted her (correct) analysis at a minute before 9 AM this morning while I’m reading it nearly 8 hours earlier. This is clearly a time paradox that avails itself of no possible resolution, since I’m sure that my frame of reference regarding time is absolute. I came to this realization after years of posting to and reading certain list-serves about mathematics education in which many participants, some of whom have Ph.Ds in mathematics or engineering (and hence are by definition smarter than I am), insist that there’s only one right way to teach mathematics (and it isn’t the way I’d like to teach it). Their absolute certainty has convinced me that relativism and, hence, relativity must be bunk.
I’ll try this on my son’s math teacher. If s/he’s anything like the ones he’s had the last two years, I likely could sell the Brooklyn Bridge while I’m at it. :)
As I’m in NY, wordpress has me posting GMT. They also give me a form of LaTeX.
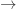
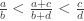
see:
Now why should I complain?
But it doesn’t seem like its GMT… 9am GMT midnight PST (and I believe 11pm PDT). But I posted my first comment around 9pm PDT, and its only 11:35PDT now… I’ll see what time the post is labeled…
Oops — I meant 8am GMT is midnight PST, and 1am PDT… So I would have thought I was posting this at 6:38am GMT.
And, in fact, I just checked that with the USNO master clock:
http://tycho.usno.navy.mil/utclock.html?
Better (?) time link:
http://www.time.gov/timezone.cgi?UTC/s/0/java
I too only found one answer, that Patricia brought the apple. What was your friend’s other solution? As for context, my first thought is a Geometry/truth tables lesson. Although it might be a fun filler for those last minutes on a crazy day (i.e. assembly, early dismissal…).
WordPress let’s you change your default time zone
I’m sending my answer without looking at any of the others. I see only one solution here, as follows:
Quentin could not be telling the truth, because if he were telling the truth, and Roger had brought the apple, then Patricia’s statement that she had not brought the apple would also be true, and we’re only allowed one true statement. So, since Quentin cannot be telling the truth, Roger must be telling the truth when he said that Quentin did not tell the truth. So, Roger is the truth-teller, and the rest are liars. Which means that Patricia lied when she said she did not bring the apple, so she must have brought the apple. (Checking, that means that Quentin lied when he said Roger brought it, Roger was telling the truth when he said Quentin lied, and Sara lied when she said Quentin brought it.)
I think most middle schoolers could solve this. Maybe even some kids younger than that.
As for context, I’d give it as something to work on after finishing the regular work of the day. Or occasionally I’ll promise to bring “grid puzzles” on a particular day (generally where I can’t do a normal lesson for scheduling reasons), and I could include logic puzzles like this one as well.
When we offer “Statement A” and “Statement A is false” we know that one of them is true. A or ~A. Quentin and Rogers statements fit this description, and one is true, and one is false.
Life gets easy. Sara lied (who cares) but so did Patricia. Done.
The problem was designed, I believe, without that analysis in mind.
nah.
on jd’s model “patricia lied”
seems to contradicts “roger did it”.
(since p’s claim was “i didn’t do it”
and this appears *true* if r *did* do it).
he’s right (of course) to conclude
that exactly one of r & q must be
the truth-teller.
so we’ll have to violate the
more-or-less taken-for-granted
[but unstated] assumption that
exactly one person brought the apple.
“p & r jointly brought the apple” works
if we’re willing to go this far to get an answer.
i say it’s spinach and i say the hell with it.
I’ll buy that (reasoning, not spinach). Problem fails to specify “exactly one bearer of fruit,” allowing multiple correct answers. But why was the answer in unrhymed verse?
What was that Vlorbik, an oblate sonnet?
but i don’t buy it *myself*!
i seem to’ve confused
“being the truth teller”
with “having brought the apple”
(or something; anyway, i got it wrong).
roger’s telling the truth;
so quintin lied (& r didn’t bring it).
also sara lied (& q didn’t bring it);
finally pat lied (& *did* bring it).
exactly one truth-teller (roger)
& exactly one apple-bringer (pat);
perfect consistency with all the conditions
(including the unstated).
so. blag. this was a good problem
after all . . . dognab it. but what the heck.
even the unapologetic must
sometimes admit mistakes.
in fact, this points at what, for me,
is one of the most attractive features
of our chosen field of study:
a pair of people can argue like heck
over some piece of math. argue, argue;
blah, blah; more argument … but then:
“oh! hey, wait! you’re right; i’m wrong.”
that hardly ever happens in other contexts.
p.s.
i’ve written in this style in e-mails
since before the days of the web.
not to simulate verse, particularly,
or even to emulate r. bucky fuller …
but, anyway at least in part,
to avoid having line breaks
that i *didn’t* want, inserted
by some random software.
also i get to avoid the shift key.
also when i go back to a comment thread
(to see if anybody’s paid me any attention)
i can easily find my own posts . . .
jorn has some remarks about
this kind of thing here.
i’m way behind on actual work.
how i love this world wide web.
pps.
if i can just cultivate this attitude of
“everybody else (rachel, jackie,
mathmom, & jd in this instance)
is wrong; i don’t even have to try
to understand them; whatever
crazy thing occurs to *me* just
*has* to be right (even if i don’t
bother to check it”, why then,
i can become a bona fide *crank*!
i’ve been more or less planning
on shooting for “raving loony”
for quite a while now. i’ve got
the “loony” bit pretty well under control,
i think, but “raving” turns out to be
somewhat more work than i’d like
(and may be hazardous to one’s
peace of mind).
getting back to work. no, really.