Ellipse question
May 22, 2007 pm31 2:24 pm
A student asks: is a circle an ellipse.
Certainly a square is a (special) rhombus, so I know what she’s getting at; the analogy is tempting.
But I also know that in the US, a parallelogram is (usually) not a trapezoid.
Anyway, can you help me answer the girl’s question?
12 Comments
leave one →
JD2718 
yes! A circle is an ellipse with eccentricity 0. In general the equation of an ellipse is (x/a)^2 + (y/b)^2 = 1; you get a circle when a=b.
I agree with Brent. To put it another way, when the two foci of an ellipse are coincident on the center, we get a circle.
I think the usual definition of ellipse is: An ellipse is the set of all points (x, y) in the plane such that the sum of the distances from (x, y) to two fixed points F_1 and F_2 is some constant. It does not say that F_1 and F_2 need to be two distinct points. If they are not, then we have a circle. btw, what time zone does your blog belong to?
Let me make 3 votes for “yes,” and also one vote that it would be more natural if a parallelogram *were* a trapezoid, except that one would more often have to say things like, “a non-parallelogram trapezoid,” which could get tiresome very quickly. (Of course, one could exclude circles from ellipses using exactly the same sorts of linguistic constructions: “the foci of the ellipse are two *distinct* points,” or “the equation of an ellipse is
*where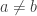 
*,” or “an ellipse is the intersection of a plane with a cone so that blah blah blah *but not perpendicular to* the axis of the cone.” I think one doesn’t make that distinction simply because there is rarely a good reason to, and “non-circular ellipse” is less of a mouthful :) .)
Hmm, I seem to have flubbed my latex — that should be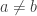
.
Okay, so now it seems to be fixed. Also, I didn’t see e’s comment, so I guess that makes me vote number 4, not vote number 3. Also also, Brent and I are both wrong on one point: we gave the general equation for an ellipse centered at the origin with axes parallel to the coordinate axes — the general equation for an ellipse in the plane is that equation plus a rotation and a translation.
I’ll add my “yes” vote to this. It’s a point I make a lot teaching Kepler’s laws (planets move in ellipses, etc). Circles are special cases of ellipses and are perfectly valid Keplerian orbits.
— Rachel
Thanks guys. My gut said a circle was a special ellipse, and yours do as well. But all the answers beg the question. What actually should count as an authoritative source for this?
JBL, on the trapezoid, I more or less agree with you. I think in British English, they use trapezium for trapezoid, and don’t limit it to exactly 2 parallel sides.
Well, it’s just a matter of convention, so anything that reasonably represents convention should do fine — mathworld, for instance, uses the construction “noncircular ellipse,” implying (although I don’t see it written explicitly as I glance over the ellipse entry) that there exist circular ellipses, i.e. that circles are ellipses.
“Trapezium” is used in my middle school texts to mean a quadrilateral with no parallel sides, sort of a catch-all for everything that does not fit into another category. They also further specify that “trapezium kite” is a trapezium with the pairs of adjacent sides the same lengths and opposite angles having the same measure. Trapezoid was defined as having “exactly one pair” of parallel sides.
Same sort of thing: Is an equilateral triangle also an isosceles triangle?
I like these “define your terms” questions… especially in middle school, modeling logical thinking and checking at the edges of what is allowed sets kids up well to start looking for counterexamples to hunches. All those SAT questions about “which column is bigger?” work on the same kind of logical skills. What about if x is zero? What about if a is negative? These are things that math teachers do all the time, without even thinking about it, but some of our kids don’t know why we even tried that example! Make sure to encourage this girl for asking!!
When we discuss a in the equation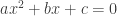
the kids quickly discover what difference it makes when a is negative vs a being positive. But yup, need to ask “What if a = 0?” That sort of question helps avoid the trap of memorizing lots of facts. Every unit, every lesson, has some of these, “let’s see if we have our brains on?” questions.
I praise good questions on the spot, this being no exception. I told them I don’t know the answer, and that I would ask. And then I came back, saying everyone who has responded had the same gut reaction as me, but that they are supplying self-made definitions of ellipse by equation that presuppose the answer they are supplying (begging the question), and that I will continue to hunt for a good answer.
One definition of ellipses doesn’t include circles: an ellipse is the set of all points whose ratio of the distance to a given point to the distance to a given line is fixed and less than 1. When the ratio is 1, you get a parabola; when it’s greater than 1, you get a hyperbola. The ratio can’t be 0, because that means the directrix is a line at infinity.