The quadratic formula
end here:
I’m feeling a little guilty. I have an accelerated class: we are covering the equivalent of Algebra II/Trig and Precalc in 3 terms, which I think is a bit fast, but doable. When these guys were finishing algebra, over a year ago, they watched the derivation of the quadratic formula, memorized the formula (if they hadn’t already) and had to apply it. Now though, second bite of the apple.
I started the derivation, then told them to work on solving for x in groups. Everyone made some progress, though only one group finished. We then slowly worked it out together.
What should you add to each side to complete the square:
So here’s the guilt part: I told them they needed to be able to recreate the derivation. My teacher training says this is not what math is about. My knowledge of calculus tells me they will thank me for the forced work with extended application of ugly algebra. We have completing the square, ok, I know, not so many applications, some, just not so many. But we also get factoring, taking square roots, adding algebraic fractions, simplifying square roots, lots of work with variables.
So what say you: punitive or worthwhile?
start there:

WORTHWHILE :)
i feel i’m predictable.
Most worthwhile.
In my advanced age, I find memory for formulae to be fallible, but concepts and methods are more easily accessible. In addition, falling back on first principles is a time-honored tradition, and the ability to do so should be stressed, IMHO.
Just make sure they know it by rote first. You use the quadratic formula too much to have to derive it every time.
If they know it by rote, and know what it’s for (finding the roots of degree-2 polynomials), they should be able to derive it pretty easily. If they know how to complete the square, that is.
They already have it memorized (from a year ago) The question is, second time around, should they be held responsible for the algebraic manipulations needed to rederive it. I told them yes, they were, but I am mulling over whether to release them from it.
The big plus may be that such skills will be useful in 2 years in calculus. The big minus is that it turns into a big chunk of yucky memorization.
The hardest step, btw, is completing the square.
how about a middle ground? do not release them, but you don’t actually have to test them on it. you could ask a question “what is an imortant ingredient of the derivation?”, but not actually ask them to do it. or better yet give them a quadratic equation that they can not solve by factoring and ask them to solve it without using the quadratic formula. then they have to demonstrate that they know how to derive the formula, but it’s little less abstract than using a,b, and c. and words “derive” and “proof” are avoided (not that i think they shouldbe).
Well, they’ll need to know how to complete the square anyway, if they continue with math. You could have them do lots of problems where they complete the square, or you could just give them the general problem. Or both.
What tends to confound students is the amount of variables. What you could do is teach them how to make simple substitutions, so that the problem looks easier. For example, when they are faced with , they could let
, they could let  and
and  , so that the equation becomes
, so that the equation becomes  . I don’t know if that will necessarily help them (it may just confuse them), but it at least separates the problem into more manageable subproblems.
. I don’t know if that will necessarily help them (it may just confuse them), but it at least separates the problem into more manageable subproblems.
I’d say it’s definitely worthwhile! Knowing where a formula comes from is essential.
I struggle with this question as well. On the one hand, yes, all the algebra is necessary and it’s good practice. On the other hand, if we say that we’re testing this we will probably end up with some kids who memorize the derivation but can’t complete the square in other contexts.
This teaching dilemma comes up again and again in trig: sin and cos add/subtract formulas, double and half angle formulas, and identities. First I want them to know the formulas. I want them to follow the derivations. Then I want them to know the derivations. And I want them to be able to re-derive as needed. Finally, I want them to apply those techniques in other situations. But how to get all the way there? How much time to spend? It’s a judgement call in each case. I’ve never tested kids on the derivation of the quadratic. But I like Jon’s idea of testing sub-problems within the derivation.
Thank you for the comments!
I am still thinking about whether or not I will really test them (in the meantime, they think they will be tested on the derivation in 2 weeks)
I want to play with Jon’s substitutions. What if m = 2k, ie ? (the back substitution at the end becomes ugly…)
? (the back substitution at the end becomes ugly…)
Finally, there is a pre-calc element to this class. I will derive all formulas, without exception, and prove all theorems.
I will make them responsible for selected derivations and selected proofs. The question becomes, which ones, and how many.
I haven’t taught used the quadratic formula since I taught math 20-odd years ago. But I can derive it quickly because I remember that it requires completing the square.
So, my vote is for teaching them to derive it. They should memorize it for the short run, but they’ll know it forever if they can derive it.
I’ll second John’s reasoning…
There are limits to how many years the details of the formula will stick in your head through rote memorization. I have re-derived it by completing the square more than a few times in the last 30 years.
Of course this requires that completing the square “make sense” enough to stick in ones head more than the sign details of the formula itself, but I think its worth it to ask them — it’s part of thinking of the students as budding mathematicians, not just kids trying to get through the Regents and the SATs
— Rachel
I think it’s worthwhile. But for what it’s worth, you can equally well ask them to prove the formula, which is somewhat easier (it involves multiplying the two solutions together, more or less). The important thing to teach is the technique of completing the square, which gets used all the time in algebra.
Among other things, it introduces the more general technique of adding and subtracting the same thing from an expression, or multiplying and dividing; what you do when you complete the square isn’t materially different from what you do when you divide two complex numbers by multiplying and dividing by the denominator’s conjugate or add and subtract an expression in a limit in order to prove the product rule in calculus.
They already found the sum and product of the roots (no need to memorize), but I think to “prove” the formula they would need to substitue both and
and 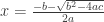 into
into 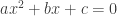 to show that they are both roots.
to show that they are both roots.
I think it’s worthwhile. I never tested my students on knowing the quadratic formula (although I did show them the derivation) but I think I should have. The bigger issue is that it teaches them what’s really important — not memorizing a bunch of formulas but understanding where things come from.
“The bigger issue is that it teaches them what’s really important — not memorizing a bunch of formulas but understanding where things come from.”
I don’t know about that. Rote memorization is extremely important in math, especially if you go on to more advanced stuff. There’s no substitute for being able to mull over a theorem or lemma in your head to really get at what it’s saying. It’s time-consuming, not to mention annoying, if you have to go back to a book every time you want to think about something.
If they know what the quadratic formula is and then what it’s for, they should be able to derive it without any instruction, really. You can teach them to memorize it, and then teach them how to derive it, but if they can’t put into words what it’s actually used for, they will never be able to connect the two. Odds are they’ll just forget the derivation. Knowing what it is and what it’s for should lend naturally to how to derive it, in my opinion.
They are sophomores, and I am informing the next two and a half years of their math education. I will definitely insist that they memorize it, and use it. I am still not certain if I will test them on the derivation, but I am leaning to “Yes.” Applying completing the square when there are no numbers will make it simpler to do when numbers are in play. And their calculus teacher will appreciate that they are a little less afraid of symbol-full expressions.
I think that requiring recreation (& hence, a true understanding) of the derivation is the ONLY way to teach the quadratic formula. Otherwise, it seems a bit like teaching a “faith based” religion. Fine for those who have a strong sense of faith but not good for proof-seeking, ratoinal-minded logical thinkers.
And indeed I tested them, and it was the right thing to do. When they learn it the first time in my school, they participate in the derivation (as an involved audience), but until, as coach says, they recreate it, it remains a nifty piece of memorization that gives them something that seems to work.
The derivation can be facilitated graphically. Draw a rectangle and label the parts. The short side is x, and the long side is b/a. The process of “Completing the Square” will now make sense, at least when the goal of finding the solution for x is reached.
I have created an extensive article about quadratic formula here:
http://math4allages.wordpress.com/2009/12/18/derivation-of-the-quadratic-formula/